练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知正方体的棱长为1，给出下列四个命题：①对角线被平面和平面三等分；②正方体的内切球，与各条棱相切的球，外接球的表面积之比为；（3）以正方体的顶点为顶点的四面体的体积都是；④正方体与以为球心，1为半径的球的公共部分的体积是，其中正确命题的序号为__________.

    【答案】①②④.

    【解析】

    根据点、直线、平面之间的位置关系的定理，以及各种空间几何体的体积计算公式，逐项判断，即可得到本题答案.

    ①如图所示，假设对角线与平面相交于点M，可得平面，所以，解得，因此对角线被平面和平面三等分，正确；

    ②易得正方体的内切球、与各条棱相切的球、外接球的半径分别为，

    因此表面积之比，正确；

    ③以为顶点的三棱锥的体积，不正确；

    ④正方体与以A为球心，1为半径的球的公共部分的体积，正确.

    故答案为：①②④

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】在平面直角坐标系中，以坐标原点为极点，轴的正半轴为极轴建立极坐标系，曲线的方程为，过点的直线的参数方程为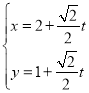（为参数）.

    （Ⅰ）求直线的普通方程与曲线的直角坐标方程；

    （Ⅱ）若直线与曲线交于、两点，求的值，并求定点到，两点的距离之积.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】假设关于某设备的使用年限x（年）和所支出的维修费用y万元有如下的统计资料：

    x

    2

    3

    4

    5

    6

    y

    2.2

    3.8

    5.5

    6.5

    7.0

    （1）画出散点图并判断是否线性相关；

    （2）如果线性相关，求线性回归方程；

    （3）估计使用年限为10年时，维修费用是多少？

    附注：①参考公式：回归方程中斜率和截距的最小二乘估计分别为；

    ②参考数据：

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下面程序框图中，已知，则输出的结果是____________.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某网购平台为了解某市居民在该平台的消费情况，从该市使用其平台且每周平均消费额超过100元的人员中随机抽取了100名，并绘制如图所示频率分布直方图，已知中间三组的人数可构成等差数列.

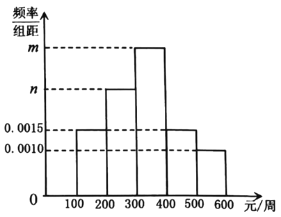
    （1）求的值；

    （2）分析人员对100名调查对象的性别进行统计发现，消费金额不低于300元的男性有20人，低于300元的男性有25人，根据统计数据完成下列列联表，并判断是否有的把握认为消费金额与性别有关？

    （3）分析人员对抽取对象每周的消费金额与年龄进一步分析，发现他们线性相关，得到回归方程.已知100名使用者的平均年龄为38岁，试判断一名年龄为25岁的年轻人每周的平均消费金额为多少.（同一组数据用该区间的中点值代替）

    列联表

    男性

    女性

    合计

    消费金额

    消费金额

    合计

    临界值表：

    0.050

    0.010

    0.001

    3.841

    6.635

    10.828

    ，其中

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设集合，.

    （1）若集合含有三个元素，且，这样的集合有多少个？所有集合中个元素之和是多少？

    （2）若集合各含有三个元素，且，，，这样的集合有多少种配对方式？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】在正方体ABCD﹣A1B1C1D1中，下列判断正确的是（ ）

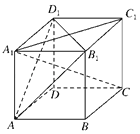
    A.A1C⊥面AB1D1B.A1C⊥面AB1C1D

    C.A1B⊥面AB1D1D.A1B⊥AD1

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数， ．

    （1）求函数的极值；

    （2）若不等式对恒成立，求的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如果函数的定义域为，且存在实常数，使得对于定义域内任意，都有成立，则称此函数具有“性质”.

    （1）判断函数是否具有“性质”，若具有“性质”，求出所有的值的集合，若不具有“性质”，请说明理由；

    （2）已知函数具有“性质”，且当时，，求函数在区间上的值域；

    （3）已知函数既具有“性质”，又具有“性质”，且当时，，若函数的图像与直线有2017个公共点，求实数的值.

    查看答案和解析>>

    同步练习册答案