练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】在如图所示的三棱锥中，底面分别是的中点．

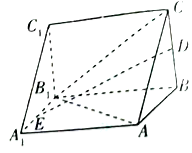
    （1）求证：平面；

    （2）若，求直线与平面所成角的正切值．

    【答案】（1）证明见解析；（2）.

    【解析】

    试题分析：（1）借助题设条件运用线面平行的判定定理求解；（2）借助题设运用直线与平面所成角的定义找出其角,再运用解三角形的方法求解.

    试题解析：（1）取的中点，连接

    在中，因为分别为的中点，

    所以平面平面，

    所以平面

    在矩形中，因为分别为的中点，

    所以平面 平面，所以平面

    因为，所以平面平面

    因为平面，所以平面

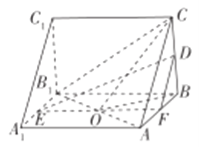
    （2）因为三棱柱为直三棱柱，所以，

    又，所以平面，

    因为，所以，

    又，所以为正三角形，

    所以，所以

    取的中点，连接，所以，所以平面，

    所以平面平面，点在平面上的射影在上，

    所以即为直线与平面所成角

    在中，，所以．．．．．．．．．12分

    （若用空间向量处理，请相应给分）

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数．

    （Ⅰ）求函数的单调区间；

    （Ⅱ）求证：①；

    ②曲线上的所有点都落在圆内．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】某校对高一年级学生寒假参加社区服务的次数进行了统计，随机抽取了名学生作为样本，得到这名学生参加社区服务的次数，根据此数据作出了频率分布统计表和频率分布直方图如下：

    （1）求表中的值和频率分布直方图中的值，并根据频率分布直方图估计该校高一学生寒假参加社区服务次数的中位数；

    （2）如果用分层抽样的方法从样本服务次数在和的人中共抽取6人，再从这6人中选2人，求2人服务次数都在的概率.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在四棱锥P﹣ABCD中，平面PAD⊥平面ABCD，AB∥DC，△PAD是等边三角形，已知AD=4， ，AB=2CD=8．

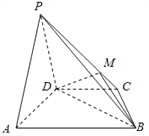
    （1）设M是PC上的一点，证明：平面MBD⊥平面PAD；

    （2）当M点位于线段PC什么位置时，PA∥平面MBD？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，在以为顶点的五面体中，O为AB的中点，

    平面， ∥， ， ， ．

    （1）在图中过点O作平面，使得∥平面，并说明理由；

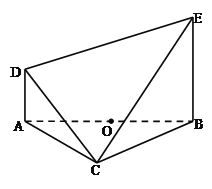
    （2）求直线DE与平面CBE所成角的正切值．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】有两个不透明的箱子，每个箱子都装有4个完全相同的小球，球上分别标有数字1,2,3,4.

    (1)甲从其中一个箱子中摸出一个球，乙从另一个箱子摸出一个球，谁摸出的球上标的数字大谁就获胜（若数字相同则为平局），求甲获胜的概率；

    (2)摸球方法与（1）同，若规定：两人摸到的球上所标数字相同甲获胜，所标数字不相同则乙获胜，这样规定公平吗？请说明理由。

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知是函数的一个极值点．

    （1）求；

    （2）求函数的单调区间；

    （3）若直线与函数的图象有3个交点，求的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数，

    （1）求函数的单调递减区间；

    （2）若关于的方程在区间上有两个不等的根，求实数的取值范围；

    （3）若存在，当时，恒有，求实数的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数， .

    （1）求函数在点点处的切线方程；

    （2）当时，求函数的极值点和极值；

    （3）当时， 恒成立，求的取值范围.

    查看答案和解析>>

    同步练习册答案