
分析 确定P的轨迹方程,即可得出结论.
解答 解:y=k(x-3)+4 必经过点Q (3,4)是以新原点O'(3,4)坐标下的y'=kx'
$f(x)=\frac{4x-11}{x-3}$是以新原点O'(3,4)坐标下的x'y′1
所以交点A,B为新原点O'下的A($\frac{1}{\sqrt{k}}$,$\sqrt{k}$),B(-$\frac{1}{\sqrt{k}}$,-$\sqrt{k}$)
PA=($\frac{1}{\sqrt{k}}$-m)+($\sqrt{k}$-n)i
PB=(-$\frac{1}{\sqrt{k}}$-m)+(-$\sqrt{k}$-n)i
|PA+PB|=|-2m-2ni|=2
|m+ni|=1
即m2+n2=1 是一个圆,即P的轨迹是以(3,4)为圆心的单位圆,
∴x2+y2的取值范围为[16,36],
故答案为[16,36].
点评 本题考查轨迹方程,考查学生的计算能力,确定P的轨迹方程是关键.


 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | {x|-1<x<3} | B. | {x|-1<x≤e} | C. | {x|0<x≤e} | D. | {x|e≤x<3} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2 | B. | 3 | C. | $\frac{18}{7}$ | D. | 14 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
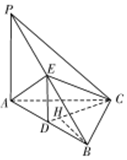 如图,已知三棱锥P-ABC中,PA⊥AC,PC⊥BC,E为PB中点,D为AB的中点,且△ABE为正三角形.
如图,已知三棱锥P-ABC中,PA⊥AC,PC⊥BC,E为PB中点,D为AB的中点,且△ABE为正三角形.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
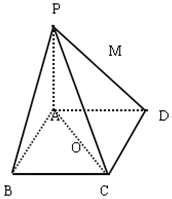 如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥面ABCD,PA=AD=4,AB=2,以AC中点O为球心,AC为直径的球面交线段PD(不含端点)于M.
如图,在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥面ABCD,PA=AD=4,AB=2,以AC中点O为球心,AC为直径的球面交线段PD(不含端点)于M.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com