
���� ��$\frac{{{a_n}+{a_{n+2}}}}{2}��{a_{n+1}}$�������Ϊan+an+2��2an+1�������Ȼ����һ��֤5�����еô𰸣�
��� �⣺����an=2n+$\frac{1}{n}$+1Ϊ����������С�����${2}^{n}+\frac{1}{n}+1+{2}^{n+2}+\frac{1}{n+2}+1��2��{2}^{n+1}+\frac{1}{n+1}+1��$�������
��${2}^{n}��\frac{-2}{n��n+1����n+2��}$���������ʽ��Ȼ����ȷ���ٲ��ǡ���������С���
����an=n2+1Ϊ����������С�����n2+1+��n+2��2+1��2��n+1��2+2��
��2��0���������ʽ��Ȼ����ȷ���ڲ��ǡ���������С���
����an=2n+1Ϊ����������С�����2n+1+2��n+2��+1��2[2��n+1��+1]��
��0��0���������ʽ��Ȼ��ȷ�����ǡ���������С���
����an=ln$\frac{n}{n+1}$Ϊ����������С�����ln$\frac{n}{n+1}$+ln$\frac{n+2}{n+3}$��2ln$\frac{n+1}{n+2}$��
��$\frac{n}{n+1}•\frac{n+2}{n+3}�ܣ�\frac{n+1}{n+2}��^{2}$�������Ҳ����2n+3��0���������ʽ��Ȼ��ȷ�����ǡ���������С���
����an=2n+$\frac{1}{n}$Ϊ����������С�����$��2n+\frac{1}{n}��+[2��n+2��+\frac{1}{n+2}]$$��2[2��n+1��+\frac{1}{n+1}]$��
��2��0���������ʽ��Ȼ����ȷ���ڲ��ǡ���������С���
�ʴ�Ϊ���ۢܣ�
���� �������¶����⣬���������еĺ������ԣ������˼������������е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2 | B�� | $\frac{4}{3}$ | C�� | $\frac{2}{3}$ | D�� | $\frac{8}{3}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
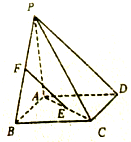 ��ͼ����P-ABCD�ĵ���ABCD�����Σ�PA�͵���ABCD��E��F�ֱ���AC��PB���е㣬PA=AB=2����BAD=120�㣮
��ͼ����P-ABCD�ĵ���ABCD�����Σ�PA�͵���ABCD��E��F�ֱ���AC��PB���е㣬PA=AB=2����BAD=120�㣮�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | c��b��a | B�� | c��a��b | C�� | b��a��c | D�� | a��b��c |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 ��ͼ����֪��Բ$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0����������Ϊ$\frac{\sqrt{3}}{2}$���ҹ��㣨$\sqrt{3}$��$\frac{1}{2}$����
��ͼ����֪��Բ$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1��a��b��0����������Ϊ$\frac{\sqrt{3}}{2}$���ҹ��㣨$\sqrt{3}$��$\frac{1}{2}$�����鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
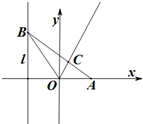 ��ͼ����֪����A��1��0������B�Ƕ�ֱ��l��x=-1�ϵĶ��㣬��BOA�Ľ�ƽ���߽�AB��C��
��ͼ����֪����A��1��0������B�Ƕ�ֱ��l��x=-1�ϵĶ��㣬��BOA�Ľ�ƽ���߽�AB��C���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com