
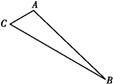
已知△ABC的三边长|AB|=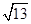 ,|BC|=4,|AC|=1,动点M满足
,|BC|=4,|AC|=1,动点M满足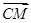 =λ
=λ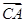 +μ
+μ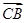 ,且λμ=
,且λμ= .
.
(1)求|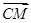 |最小值,并指出此时
|最小值,并指出此时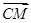 与
与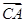 ,
,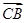 的夹角;
的夹角;
(2)是否存在两定点F1,F2使||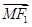 |-|
|-|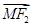 ||恒为常数k?若存在,指出常数k的值,若不存在,说明理由.
||恒为常数k?若存在,指出常数k的值,若不存在,说明理由.
(1) 
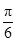 或
或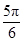 (2) 存在 k=2
(2) 存在 k=2
解析解:(1)由余弦定理知:
cos∠ACB=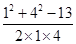 =
= ⇒∠ACB=
⇒∠ACB=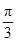 .
.
因为|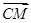 |2=
|2=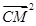 =(λ
=(λ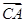 +μ
+μ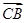 )2
)2
=λ2+16μ2+2λμ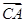 ·
·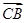
=λ2+16μ2+1≥3.
所以|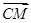 |≥
|≥ ,当且仅当λ=±1时,“=”成立.
,当且仅当λ=±1时,“=”成立.
故|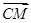 |的最小值是
|的最小值是 ,
,
此时<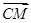 ,
,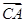 >=<
>=<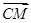 ,
,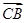 >=
>=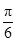 或
或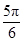 .
.
(2)以C为坐标原点,∠ACB的平分线所在直线为x轴建立直角坐标系(如图),则A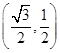 ,B(2
,B(2 ,-2),
,-2),
设动点M(x,y),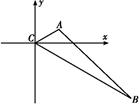
因为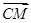 =λ
=λ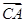 +μ
+μ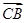 ,
,
所以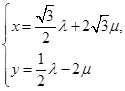 ⇒
⇒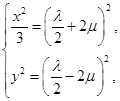
再由λμ= 知
知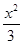 -y2=1,
-y2=1,
所以,动点M的轨迹是以F1(-2,0),F2(2,0)为焦点,实轴长为2 的双曲线,
的双曲线,
即存在两定点F1(-2,0),F2(2,0)使||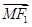 |-|
|-|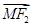 ||恒为常数2
||恒为常数2 ,即k=2
,即k=2 .
.


科目:高中数学 来源: 题型:解答题
已知向量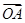 =(3,-4),
=(3,-4), =(6,-3),
=(6,-3),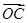 =(5-m,-3-m).
=(5-m,-3-m).
(1)若点A,B,C不能构成三角形,求实数m满足的条件;
若△ABC为直角三角形,求实数m的值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
如图,在平面斜坐标系xOy中,∠xOy=60°,平面上任一点P关于斜坐标系的斜坐标是这样定义的:若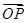 =xe1+ye2(其中e1、e2分别为与x轴、y轴同方向的单位向量),则P点斜坐标为(x,y).
=xe1+ye2(其中e1、e2分别为与x轴、y轴同方向的单位向量),则P点斜坐标为(x,y).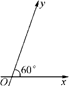
(1)若P点斜坐标为(2,-2),求P到O的距离|PO|;
(2)求以O为圆心,1为半径的圆在斜坐标系xOy中的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知关于x的方程:x2-(6+i)x+9+ai=0(a∈R)有实数根b.
(1)求实数a,b的值.
(2)若复数满足|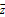 -a-bi|-2|z|=0,求z为何值时,|z|有最小值,并求出|z|的最小值.
-a-bi|-2|z|=0,求z为何值时,|z|有最小值,并求出|z|的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知四点A(x,0),B(2x,1),C(2,x),D(6,2x).
(1)求实数x,使两向量 ,
, 共线.
共线.
(2)当两向量 与
与 共线时,A,B,C,D四点是否在同一条直线上?
共线时,A,B,C,D四点是否在同一条直线上?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com