
| A. | $\frac{{\sqrt{6}}}{3}$ | B. | 2 | C. | $\frac{2}{3}$ | D. | $\frac{{\sqrt{6}}}{3}$或2 |
分析 根据题意,由$\overrightarrow a=({1,-2})和\overrightarrow b=({-m,6})$共线,结合向量平行的可得1×6-(-2)×(-m)=0,解可得m=3,可得该圆锥曲线为椭圆,由椭圆的几何性质可得c的值,由离心率公式计算可得答案.
解答 解:根据题意,若$\overrightarrow a=({1,-2})和\overrightarrow b=({-m,6})$共线,
则有1×6-(-2)×(-m)=0,解可得m=3,
则圆锥曲线的方程为:$\frac{{x}^{2}}{3}$+y2=1,为焦点在x轴上的椭圆,且a=$\sqrt{3}$,b=1;
则c=$\sqrt{3-1}$=$\sqrt{2}$,
其离心率e=$\frac{c}{a}$=$\frac{\sqrt{2}}{\sqrt{3}}$=$\frac{\sqrt{6}}{3}$;
故选:A.
点评 本题考查椭圆的几何性质,关键是求出m的值,确定圆锥曲线的类型.


科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -1 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
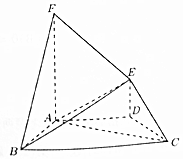 在如图所示的多面体中,DE⊥平面ABCD,AF∥DE,AD∥BC,AB=CD,∠ABC=60°,BC=2AD=4DE=4.
在如图所示的多面体中,DE⊥平面ABCD,AF∥DE,AD∥BC,AB=CD,∠ABC=60°,BC=2AD=4DE=4.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
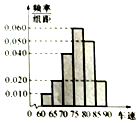 交警随机抽取了途经某服务站的40辆小型轿车在经过某区间路段的车速(单位:km/h),现将其分成六组为[60,65),[65,70),[70,75),[75,80),[80,85),[85,90]后得到如图所示的频率分布直方图.
交警随机抽取了途经某服务站的40辆小型轿车在经过某区间路段的车速(单位:km/h),现将其分成六组为[60,65),[65,70),[70,75),[75,80),[80,85),[85,90]后得到如图所示的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com