
分析 利用向量坐标运算性质、向量共线定理即可得出.
解答 解:$\overrightarrow{a}$+2$\overrightarrow{b}$=(2m-1,4),2$\overrightarrow{a}$-$\overrightarrow{b}$=(-2-m,3),
∵$\overrightarrow{a}$+2$\overrightarrow{b}$与2$\overrightarrow{a}$-$\overrightarrow{b}$平行,∴4(-2-m)-3(2m-1)=0,
解得m=-$\frac{1}{2}$,
则$\overrightarrow{a}$+$\overrightarrow{b}$=$(-\frac{3}{2},3)$.
故答案为:$(-\frac{3}{2},3)$.
点评 本题考查了向量坐标运算性质、向量共线定理,考查了推理能力与计算能力,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | $\frac{{\sqrt{6}}}{3}$ | B. | 2 | C. | $\frac{2}{3}$ | D. | $\frac{{\sqrt{6}}}{3}$或2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
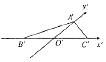 如图,△A'B'C'是△ABC用“斜二测画法”画出的直观图,其中O'B'=O'C'=1,O'A'=$\frac{{\sqrt{3}}}{2}$,那么△ABC是一个( )
如图,△A'B'C'是△ABC用“斜二测画法”画出的直观图,其中O'B'=O'C'=1,O'A'=$\frac{{\sqrt{3}}}{2}$,那么△ABC是一个( )| A. | 等边三角形 | B. | 直角三角形 | ||
| C. | 钝角三角形 | D. | 三边互不相等的三角形 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 5,10,15 | B. | 3,18,9 | C. | 3,10,17 | D. | 5,9,16 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=f(x)在区间(0,0.4)上递减 | B. | y=f(x)在区间(0.35,1)上递减 | ||
| C. | y=f(x)的最小值为f(0.4) | D. | y=f(x)在(0.3,0.4)上有最小值 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $f(x)=\frac{{{e^x}-1}}{{{x^2}-1}}$ | B. | $f(x)=\frac{e^x}{{{x^2}-1}}$ | C. | $f(x)=\frac{{{x^3}+x+1}}{{{x^2}-1}}$ | D. | $f(x)=\frac{{{x^4}+x+1}}{{{x^2}-1}}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com