
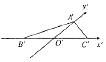
 如图,△A'B'C'是△ABC用“斜二测画法”画出的直观图,其中O'B'=O'C'=1,O'A'=$\frac{{\sqrt{3}}}{2}$,那么△ABC是一个( )
如图,△A'B'C'是△ABC用“斜二测画法”画出的直观图,其中O'B'=O'C'=1,O'A'=$\frac{{\sqrt{3}}}{2}$,那么△ABC是一个( )| A. | 等边三角形 | B. | 直角三角形 | ||
| C. | 钝角三角形 | D. | 三边互不相等的三角形 |
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:高中数学 来源: 题型:选择题
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
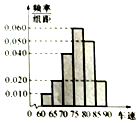 交警随机抽取了途经某服务站的40辆小型轿车在经过某区间路段的车速(单位:km/h),现将其分成六组为[60,65),[65,70),[70,75),[75,80),[80,85),[85,90]后得到如图所示的频率分布直方图.
交警随机抽取了途经某服务站的40辆小型轿车在经过某区间路段的车速(单位:km/h),现将其分成六组为[60,65),[65,70),[70,75),[75,80),[80,85),[85,90]后得到如图所示的频率分布直方图.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充分必要条件 | D. | 既不充分又不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
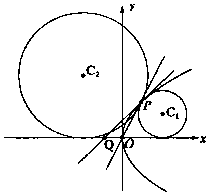 如图所示,在直角坐标系xOy中,抛物线C:y2=4x,Q(-1,0),设点P是第一象限内抛物线C上一点,且PQ为抛物线C的切线.
如图所示,在直角坐标系xOy中,抛物线C:y2=4x,Q(-1,0),设点P是第一象限内抛物线C上一点,且PQ为抛物线C的切线.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com