
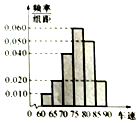
 ���������ȡ��;��ij����վ��40��С�ͽγ��ھ���ij����·�εij��٣���λ��km/h�����ֽ���ֳ�����Ϊ[60��65����[65��70����[70��75����[75��80����[80��85����[85��90]��õ���ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ��
���������ȡ��;��ij����վ��40��С�ͽγ��ھ���ij����·�εij��٣���λ��km/h�����ֽ���ֳ�����Ϊ[60��65����[65��70����[70��75����[75��80����[80��85����[85��90]��õ���ͼ��ʾ��Ƶ�ʷֲ�ֱ��ͼ������ ������Ƶ�ʺ�Ϊ1������ٶ���70km/h���ϵ�Ƶ�ʼ��ɣ�
�������40�����г�����[60��65���Լ�[65��70���ڵij�����
�����оٷ���������¼����������Ӧ�ĸ���ֵ��
��� �⣺������Ƶ�ʷֲ�ֱ��ͼ�������ٶ���70km/h���ϵ�Ƶ��Ϊ
1-��0.010+0.020����10=0.7��
�����ٶ���70km/h���ϵĸ�����0.7��
������40�����У�������[60��70���Ĺ���5����0.01+0.02����40=6����
������[65��70������5��0.02��40=4������ΪA��B��C��D��
��[60��65������5��0.01��40=2������Ϊa��b��
�ӳ�����[60��70������6�������������ȡ2�������ܽ����
AB��AC��AD��Aa��Ab��BC��BD��Ba��Bb��
CD��Ca��Cb��Da��Db��ab��15�ֲ�ͬ�Ľ����
���г����2��������������һ����[60��65���ڵĽ����
Aa��Ab��Ba��Bb��Ca��Cb��Da��Db��ab��9�֣�
������ĸ���ΪP=$\frac{9}{15}$=$\frac{3}{5}$��
���� ���⿼����Ƶ�ʷֲ�ֱ��ͼ��ͳ�ƺ��ʵļ������⣬�ǻ�����Ŀ��


 ����ѧ��Ӯ�����ϵ�д�
����ѧ��Ӯ�����ϵ�д� ѧ���쳵�����ּ��������ҵ�½����������ϵ�д�
ѧ���쳵�����ּ��������ҵ�½����������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | һ�������� | B�� | һ����ż�� | ||
| C�� | ����������Ҳ������ż�� | D�� | �����ж϶�����ȷ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{{\sqrt{6}}}{3}$ | B�� | 2 | C�� | $\frac{2}{3}$ | D�� | $\frac{{\sqrt{6}}}{3}$��2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | a��b��c | B�� | a��c��b | C�� | c��a��b | D�� | c��b��a |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\frac{1}{4}$ | B�� | 4 | C�� | $\frac{1}{8}$ | D�� | 8 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
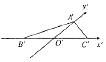 ��ͼ����A'B'C'�ǡ�ABC�á�б���⻭����������ֱ��ͼ������O'B'=O'C'=1��O'A'=$\frac{{\sqrt{3}}}{2}$����ô��ABC��һ����������
��ͼ����A'B'C'�ǡ�ABC�á�б���⻭����������ֱ��ͼ������O'B'=O'C'=1��O'A'=$\frac{{\sqrt{3}}}{2}$����ô��ABC��һ����������| A�� | �ȱ������� | B�� | ֱ�������� | ||
| C�� | �۽������� | D�� | ��������ȵ������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����

| A�� | $f��x��=\frac{{{e^x}-1}}{{{x^2}-1}}$ | B�� | $f��x��=\frac{e^x}{{{x^2}-1}}$ | C�� | $f��x��=\frac{{{x^3}+x+1}}{{{x^2}-1}}$ | D�� | $f��x��=\frac{{{x^4}+x+1}}{{{x^2}-1}}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com