练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    10．若函数y=ax在区间[0，3]上的最大值和最小值的和为$\frac{9}{8}$，则函数y=logax在区间$[{\frac{1}{4}，2}]$上的最小值是（　　）
    A．-2B．-1C．1D．2

    分析 先根据指数函数的单调性求出a的值，再根据对数函数的性质即可求出答案．

    解答 解：∵函数y=ax在区间[0，3]上的最大值和最小值的和为$\frac{9}{8}$，
    ∴1+a3=$\frac{9}{8}$，
    解得a=$\frac{1}{2}$，a=-$\frac{1}{2}$（舍去），
    ∴y=log$\frac{1}{2}$x在区间[$\frac{1}{4}$，2]上为减函数，
    ∴ymin=log$\frac{1}{2}$2=-1，
    故选：B

    点评 本题考查了指数函数和对数函数的单调性，属于基础题．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：解答题

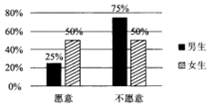    14．2017年1月1日，作为贵阳市打造“千园之城”27个示范性公元之一的泉湖公园正式开园，元旦期间，为了活跃气氛，主办方设置了水上挑战项目向全体市民开放，现从到公园游览的市民中随机抽取了60名男生和40名女生共100人进行调查，统计出100名市民中愿意接受挑战和不愿意接受挑战的男女生比例情况，具体数据如图表：
    （1）根据条件完成下列2×2列联表，并判断是否在犯错误的概率不超过1%的情况下愿意接受挑战与性别有关？
      愿意 不愿意 总计
     男生   
     女生   
     总计   
    （2）现用分层抽样的方法从愿意接受挑战的市民中选取7名挑战者，再从中抽取2人参加挑战，求抽取的2人中至少有一名男生的概率．
    参考公式与数据：
     P（K2≥k0） 0.1 0.05 0.025 0.01
     k0 2.7063.841 5.024 6.635 
    K2=$\frac{n（ad-bc）^{2}}{（a+b）（c+d）（a+c）（b+d）}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    1．函数f（x）=x2-27有极小值为-27．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    18．下列结论不正确的是（　　）
    A．若ab＞bc，则a＞cB．若a3＞b3，则a＞b
    C．若a＞b，c＜0，则ac＜bcD．若$\sqrt{a}$＜$\sqrt{b}$，则a＞b

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    5．对数列{an}，{bn}，若区间[an，bn]满足下列条件：
    ①$[{{a_{n+1}}，{b_{n+1}}}]?[{{a_n}，{b_n}}]（{n∈{N^*}}）$；
    ②$\lim_{n→+∞}（{{b_n}-{a_n}}）=0$；则[an，bn]为区间套，
    下列可以构成区间套的数列是（　　）
    A．${a_n}={（{\frac{1}{2}}）^n}，{b_n}={（{\frac{2}{3}}）^n}$B．${a_n}={（{\frac{1}{3}}）^n}，{b_n}=\frac{n}{{{n^2}+1}}$
    C．${a_n}=\frac{n-1}{n}，{b_n}=1+{（{\frac{1}{3}}）^n}$D．${a_n}=\frac{n+3}{n+2}，{b_n}=\frac{n+2}{n+1}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    15．△ABC的内角A，B，C所对的边分别是a，b，c，向量$\overrightarrow m=（{b，-\sqrt{3}a}）$与$\overrightarrow n=（{cosA，sinB}）$垂直．
    （1）求A；
    （2）若B+$\frac{π}{12}$=A，a=2，求△ABC的面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    2．函数f（x）=ax-（k-1）a-x（a＞0且a≠1）是定义域为R的奇函数．
    （1）求k的值；
    （2）若f（1）＜0，试分析判断y=f（x）的单调性（不需证明），并求使不等式f（x2+tx）+f（4-x）＜0恒成立的t的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    19．一个命题与它的逆命题、否命题、逆否命题这四个命题中，真命题的个数（　　）
    A．一定是奇数B．一定是偶数
    C．可能是奇数也可能是偶数D．上述判断都不正确

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    20．已知$\overrightarrow a=（{1，-2}）和\overrightarrow b=（{-m，6}）$共线，则圆锥曲线$\frac{{x}^{2}}{m}$+y2=1的离心率为（　　）
    A．$\frac{{\sqrt{6}}}{3}$B．2C．$\frac{2}{3}$D．$\frac{{\sqrt{6}}}{3}$或2

    查看答案和解析>>

    同步练习册答案