考点:棱柱、棱锥、棱台的体积,直线与平面垂直的性质
专题:空间位置关系与距离
分析:(1)补全四棱柱ABCD-A1B1C1D1,得到四棱柱ABCD-A1B1C1D1是正方体,证出A1C1⊥平面BDD1;即可证出BD1⊥A1C1;
(2)用正方体的体积减去三棱锥的体积,得出几何体的体积.
解答:
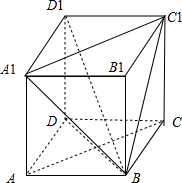
解:(1)证明:连接AC,补全四棱柱ABCD-A
1B
1C
1D
1,如图所示;
∵四边形ABCD,A
1ADD
1,DCC
1D
1均为边长为1的正方形,
∴四棱柱ABCD-A
1B
1C
1D
1是正方体,
∴DD
1⊥平面ABCD,
又AC?平面ABCD,∴DD
1⊥AC,
∵AC⊥BD,且BD∩DD
1=D,∴AC⊥平面BDD
1,
又∵AA
1∥DD
1∥CC
1,且AA
1=DD
1=CC
1,
∴四边形ACC
1A
1是平行四边形,
∴A
1C
1∥AC,
∴A
1C
1⊥平面BDD
1;
又∵BD
1⊥?平面BDD
1,
∴BD
1⊥A
1C
1;
(2)该几何体的体积是
V=
V正方体ABCD-A1B1C1D1-
V三棱锥B-A1B1C1=1
3-
•
•1
2•1
=
.
点评:本题考查了空间中的垂直于平行的判断与性质的问题,也考查了求空间几何体的体积的问题,解题的关键是补全正方体,是中档题.

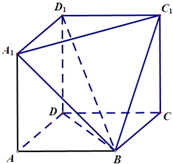 如图,在几何体ABCD-A1D1C1中,四边形ABCD,A1ADD1,DCC1D1均为边长为1的正方形.
如图,在几何体ABCD-A1D1C1中,四边形ABCD,A1ADD1,DCC1D1均为边长为1的正方形. 解:(1)证明:连接AC,补全四棱柱ABCD-A1B1C1D1,如图所示;
解:(1)证明:连接AC,补全四棱柱ABCD-A1B1C1D1,如图所示;

 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案 期末集结号系列答案
期末集结号系列答案