
| A. | ${(x-2)^2}+{(y+\frac{3}{2})^2}=\frac{25}{4}$ | B. | ${(x-2)^2}+{(y-\frac{3}{2})^2}=\frac{25}{4}$ | ||
| C. | ${(x+2)^2}+{(y-\frac{3}{2})^2}=\frac{25}{4}$ | D. | ${(x+2)^2}+{(y+\frac{3}{2})^2}=\frac{25}{4}$ |
分析 设出圆的圆心坐标与半径,利用已知条件列出方程组,求出圆的圆心坐标与半径,即可得到圆的方程.
解答 解:设圆的圆心坐标(a,b),半径为r,
因为圆C经过坐标原点和点(4,0),且与直线y=1相切,
所以$\left\{\begin{array}{l}{{a}^{2}+{b}^{2}={r}^{2}}\\{(a-4)^{2}+{b}^{2}={r}^{2}}\\{|b-1|=r}\end{array}\right.$,
解得a=2,b=-$\frac{3}{2}$,r=$\frac{5}{2}$,
所求圆的方程为:${(x-2)^2}+{(y+\frac{3}{2})^2}=\frac{25}{4}$.
故选A.
点评 本题考查圆的标准方程的求法,列出方程组是解题的关键,考查计算能力.


 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案科目:高中数学 来源: 题型:选择题
| A. | 一定单调递增 | B. | 一定没有单调减区间 | ||
| C. | 可能没有单调增区间 | D. | 一定没有单调增区间 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{4}{9}$ | B. | $\frac{5}{9}$ | C. | $\frac{2}{3}$ | D. | $\frac{1}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
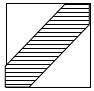 如图,在边长为25cm的正方形中挖去边长为18cm的两个等腰直角三角形,现有均匀的粒子散落在正方形中,问粒子落在中间带形区域的概率是多少$\frac{301}{625}$.
如图,在边长为25cm的正方形中挖去边长为18cm的两个等腰直角三角形,现有均匀的粒子散落在正方形中,问粒子落在中间带形区域的概率是多少$\frac{301}{625}$.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com