
分析 (1)联立两个解析式,得到交点,利用两点距离公式得到截得线段的长.
(2)由A对应的参数,得到的参数方程,由此得到普通方程.
解答 解:(1)当a=$\frac{π}{3}$时,C1的普通方程为y=$\sqrt{3}$(x-1),C2的普通方程为x2+y2=1.
联立方程组$\left\{\begin{array}{l}{y=\sqrt{3}(x-1)}\\{{x}^{2}+{y}^{2}=1}\end{array}\right.$,
解得C1与C2的交点为(1,0)与($\frac{1}{2}$,-$\frac{\sqrt{3}}{2}$).
所以,C1被C2截得的线段的长为1.
(2)将C1的参数方程代C2的普通方程得t2+2tcosα=0,
∴A点对应的参数t=$\frac{{t}_{1}+{t}_{2}}{2}$=-cosα,
∴A点坐标为(sin2α,-cosαsinα).
故当α变化时,A点轨迹的参数方程为:$\left\{\begin{array}{l}{x=si{n}^{2}α}\\{y=-sinαcosα}\end{array}\right.$(α为参数).
因此,A点轨迹的普通方程为(x-$\frac{1}{2}$)2+y2=$\frac{1}{4}$.
故A点轨迹是以($\frac{1}{2}$,0)为圆心,半径为$\frac{1}{2}$的圆.
点评 本题考查联立解析式,两点距离公式,由对应的参数,得到的参数方程.


科目:高中数学 来源: 题型:选择题
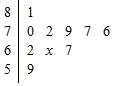 高三某班级10名同学的物理期中考试成绩分布的茎叶图如图,其中一名同学的成绩有误,其末位数记为x,已知这10名学生成绩的中位数与平均数相同,则x的值为( )
高三某班级10名同学的物理期中考试成绩分布的茎叶图如图,其中一名同学的成绩有误,其末位数记为x,已知这10名学生成绩的中位数与平均数相同,则x的值为( )| A. | 3 | B. | 5 | C. | 7 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com