
分析 (1)求出f(x)的导数,根据函数的单调性结合二次函数的性质得到关于a的不等式组,解出即可;
(2)求出a<-2$\sqrt{2}$时,f(x1)→-$\frac{3+ln2}{2}$,问题转化为m+f(x)极大值=m+f(x1)<0恒成立,求出m的最大值即可.
解答 解:(1)f(x)=x2+ax+lnx的定义域是(0,+∞),
f′(x)=2x+a+$\frac{1}{x}$=$\frac{{2x}^{2}+ax+1}{x}$,
若函数f(x)不单调,
则g(x)=2x2+ax+1只需满足:
$\left\{\begin{array}{l}{△{=a}^{2}-8>0}\\{{x}_{2}=\frac{-a+\sqrt{{a}^{2}-8}}{4}>0}\end{array}\right.$,
解得:a<-2$\sqrt{2}$,
(2)x→0时,f(x)→-∞,x→+∞时,f(x)→+∞,
当a<-2$\sqrt{2}$时,f′(x)=2x+a+$\frac{1}{x}$=0的解可设为:
x1=$\frac{-a-\sqrt{{a}^{2}-8}}{4}$,x2=$\frac{-a+\sqrt{{a}^{2}-8}}{4}$,
显然x1,x2都是正数,
且0<x1=$\frac{-a-\sqrt{{a}^{2}-8}}{4}$=$\frac{2}{-a+\sqrt{{a}^{2}-8}}$<$\frac{2}{-a}$<$\frac{2}{2\sqrt{2}}$=$\frac{\sqrt{2}}{2}$,
易知:ax1=-1-2${{x}_{1}}^{2}$,
故f(x1)=${{x}_{1}}^{2}$+ax1+lnx1=-1-${{x}_{1}}^{2}$+lnx1,
令g(x)=-1-x2+lnx,(0<x<$\frac{\sqrt{2}}{2}$),
g′(x)=$\frac{1-{2x}^{2}}{x}$>0,∴函数g(x)是增函数,
故f(x1)=-1-${{x}_{1}}^{2}$+lnx1<-1-$\frac{1}{2}$+ln$\frac{\sqrt{2}}{2}$=-$\frac{3+ln2}{2}$,
(易验证,当a→-2$\sqrt{2}$时,f(x1)→-$\frac{3+ln2}{2}$),
易知,函数f(x)+m在(0,x1)上是增函数,在(x1,x2)上是减函数,在(x2,+∞)上是增函数,
故f(x)极大值=f(x1),
如果对一切a<-2$\sqrt{2}$,函数f(x)+m至多有一个零点,
则,m+f(x)极大值=m+f(x1)<0恒成立,
因此,m-$\frac{3+ln2}{2}$≤0?m≤$\frac{3+ln2}{2}$,
故m的最大值是$\frac{3+ln2}{2}$.
点评 本题考查了函数的单调性、最值问题,考查转化思想以及函数恒成立问题,是一道综合题.


科目:高中数学 来源: 题型:选择题
| A. |  | B. | 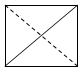 | C. | 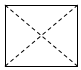 | D. |  |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
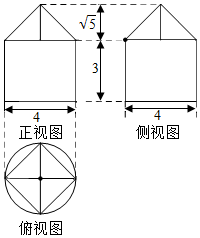
| A. | 12π+$\frac{{8\sqrt{5}}}{3}$ | B. | 4π+$\frac{{8\sqrt{5}}}{3}$ | C. | 12π+8$\sqrt{5}$ | D. | 4π+8$\sqrt{5}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -4 | B. | -1 | C. | 1 | D. | 4 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com