
分析 由题意可得:m>f(x)min,利用导数研究函数的单调性极值与最值即可得出.
解答 解:至少存在一个x0∈[-1,2]时,f(x0)<m成立,∴m>f(x)min.
| x | $[-1,-\frac{2}{3})$ | $-\frac{2}{3}$ | $(-\frac{2}{3},1)$ | 1 | (1,2] |
| f′(x) | + | 0 | - | 0 | + |
| f(x) | 单调递增 | 极大值 | 单调递减 | 极小值 | 单调递增 |
点评 本题考查了微积分基本定理、二项式定理的应用,考查了推理能力与计算能力,属于中档题.


科目:高中数学 来源: 题型:选择题
| A. | {x|x>-2} | B. | {x|x<2} | C. | {x|-2<x<2} | D. | {x|x>-2,x≠1} |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=sin($\frac{1}{2}$x+$\frac{π}{6}}$),x∈R | B. | y=sin($\frac{1}{2}$x+$\frac{π}{12}$),x∈R | ||
| C. | y=sin(2x+$\frac{π}{3}$),x∈R | D. | y=sin(2x+$\frac{π}{6}$),x∈R |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
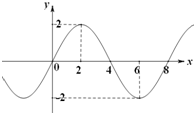 函数f(x)=Asin(ωx+ϕ)(其中A>0,ω>0)的部分图象如图所示,则f(2)+f(3)+…+f(2016)的值为( )
函数f(x)=Asin(ωx+ϕ)(其中A>0,ω>0)的部分图象如图所示,则f(2)+f(3)+…+f(2016)的值为( )| A. | $\sqrt{2}$ | B. | $2+\sqrt{2}$ | C. | 0 | D. | $-\sqrt{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| ωx+φ | 0 | $\frac{π}{2}$ | π | $\frac{3π}{2}$ | 2π |
| x | $\frac{π}{3}$ | $\frac{7π}{12}$ | |||
| Asin(ωx+φ) | 3 | 0 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com