
分析 进制转换为十进制的方法是依次累加各位数字上的数×该数位的权重;利用“除k取余法”是将十进制数除以4,然后将商继续除以4,直到商为0,然后将依次所得的余数倒序排列即可得到答案.
用辗转相除的方法求两个数字的最大公约数,把其中较大的数字写成较小数字的整数倍和余数的和的形式,以此类推,得到余数为0的结果,得到最大公约数.
解答 解:10101(2)=1×20+0×21+1×22+0×23+1×24=21,
21÷4=5…1
5÷4=1…1
1÷4=0…1
故21(10)=111(4);
∵918=714×1+204,
714=204×3+102,
204=102×2,
所以918和714的最大公约数是102.
故答案为:111(4),102.
点评 本题考查用辗转相除法求两个数字的最大公约数,考查了进位制换算的方法--除K取余法,由二进制转化为十进制的方法,我们只要依次累加各位数字上的数×该数位的权重,即可得到结果.


科目:高中数学 来源: 题型:选择题
| A. | $\overrightarrow{CA}$ | B. | $\overrightarrow{AC}$ | C. | $\overrightarrow{A{C}_{1}}$ | D. | $\overrightarrow{A{B}_{1}}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
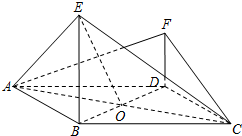 如图所示,四边形ABCD是边长为4菱形,O是AC与BD的交点,∠ABC=120°,E,F是平面ABCD同一侧的两点,BE⊥平面ABCD,DF⊥平面ABCD,BE=2DF=2$\sqrt{2}$.
如图所示,四边形ABCD是边长为4菱形,O是AC与BD的交点,∠ABC=120°,E,F是平面ABCD同一侧的两点,BE⊥平面ABCD,DF⊥平面ABCD,BE=2DF=2$\sqrt{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -5 | B. | -9 | C. | -7 | D. | -1 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
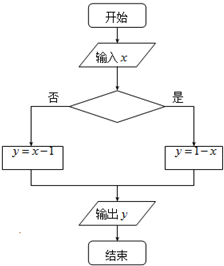 在如图所示的求函数f(x)=|x-1|的函数值的程序框图中,有六名学生在空白处的判断框内填入的条件分别是:①x≥1;②x>1;③x≤1;④x<1;⑤x≥0;⑥x≤0,其中正确的个数是( )
在如图所示的求函数f(x)=|x-1|的函数值的程序框图中,有六名学生在空白处的判断框内填入的条件分别是:①x≥1;②x>1;③x≤1;④x<1;⑤x≥0;⑥x≤0,其中正确的个数是( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
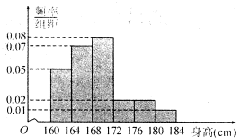 某市一次全市高中男生身高统计调查数据显示:全市100 000名男生的身高服从正态分布N(168,16).现从某学校高三年级男生中随机抽取50名测量身高,测量发现被测学生身高全部介于160cm和184cm之间,将测量结果按如下方式分成6组:第一组[160,164],第二组[164,168],组方法得到的频率分布直方图.
某市一次全市高中男生身高统计调查数据显示:全市100 000名男生的身高服从正态分布N(168,16).现从某学校高三年级男生中随机抽取50名测量身高,测量发现被测学生身高全部介于160cm和184cm之间,将测量结果按如下方式分成6组:第一组[160,164],第二组[164,168],组方法得到的频率分布直方图.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com