
分析 (1)设椭圆方程为mx2+ny2=1,m>0,n>0,m≠n,利用待定系数法能求出椭圆E的方程.
(2)设A(x1,y1),B(x2,y2),则$\frac{{{x}_{1}}^{2}}{2}+{{y}_{1}}^{2}$=1,$\frac{{{x}_{2}}^{2}}{2}+{{y}_{2}}^{2}$=1,利用点差法能证明k1+k2=0.
(3)当l与y轴平行时,设直线l与椭圆相交于C、D两点,设Q(x0,0),由已知推导出${x}_{0}=\frac{2}{t}$,从而得到存在不同于点P不同的定点Q满足条件,则Q点坐标只可能为($\frac{2}{t}$,0).再证明对任意直线l,均有$\frac{QA}{QB}=\frac{PA}{PB}$.
解答 解:(1)设椭圆方程为mx2+ny2=1,m>0,n>0,m≠n,
∵椭圆E经过两点(1,$\frac{\sqrt{2}}{2}$),($\frac{\sqrt{2}}{2}$,$\frac{\sqrt{3}}{2}$),
∴$\left\{\begin{array}{l}{m+\frac{1}{2}n=1}\\{\frac{1}{2}m+\frac{3}{4}n=1}\end{array}\right.$,解得m=$\frac{1}{2}$,n=1,
∴椭圆E的方程为$\frac{{x}^{2}}{2}+{y}^{2}$=1.
(2)设A(x1,y1),B(x2,y2),则$\frac{{{x}_{1}}^{2}}{2}+{{y}_{1}}^{2}$=1,$\frac{{{x}_{2}}^{2}}{2}+{{y}_{2}}^{2}$=1,
由题意P(1,0),Q(2,0),
∵$\overrightarrow{AP}$∥$\overrightarrow{BP}$,∴(x1-1,y1)∥(x2-1,y2),
∴x1y2-x2y1=y1-y2,
∵(x1y2-x2y1)(x1y2+x2y1)=${{x}_{1}}^{2}{{y}_{2}}^{2}-{{x}_{2}}^{2}{{y}_{1}}^{2}$
=(2-y12)${{y}_{2}}^{2}$-(2-${{y}_{2}}^{2}$)${{y}_{1}}^{2}$=$2{{y}_{2}}^{2}-2{{y}_{1}}^{2}$,
∴(x1y2+x2y1)(y1-y2)=${{2y}_{2}}^{2}-2{{y}_{1}}^{2}$=2(y1-y2)(y1+y2),
若y1=y2,则k1=k2=0,结论成立.
若y1≠y2,则x1y2+x2y1=2(y1+y2),
∴${k}_{1}+{k}_{2}=\frac{{y}_{1}}{{x}_{1}-2}+\frac{{y}_{2}}{{x}_{2}-2}$=$\frac{{x}_{1}{y}_{2}+{x}_{2}{y}_{1}-2({y}_{1}+{y}_{2})}{({x}_{1}-2)({x}_{2}-2)}$=0.
(3)当l与y轴平行时,设直线l与椭圆相交于C、D两点,
如果存在定点Q满足条件,则有$\frac{QC}{QD}$=$\frac{PC}{PD}$,
∴QC=QD,∴Q在x轴上,设Q(x0,0),
当直线l与y轴垂直时,设直线l与椭圆相交于M,N两点,
则M,N的坐标分别为($\sqrt{2}$,0),(-$\sqrt{2}$,0),
由$\frac{OM}{ON}=\frac{PM}{PN}$,有|$\frac{{x}_{0}-\sqrt{2}}{{x}_{0}+\sqrt{2}}$|=|$\frac{\sqrt{2}-t}{\sqrt{2}+t}$|,
解得${x}_{0}=\frac{2}{t}$,
∴若存在不同于点P不同的定点Q满足条件,则Q点坐标只可能为($\frac{2}{t}$,0).
下面证明:对任意直线l,均有$\frac{QA}{QB}=\frac{PA}{PB}$,
记直线AQ的斜率为k1,直线BQ的斜率为k2,
设A(x1,y1),B(x2,y2),则$\frac{{{x}_{1}}^{2}}{2}+{{y}_{1}}^{2}$=1,$\frac{{{x}_{2}}^{2}}{2}+{{y}_{2}}^{2}$=1.
由题意P(t,0),Q($\frac{2}{t}$,0),
∵$\overrightarrow{AP}$∥$\overrightarrow{BP}$,∴(x1-t,y1)∥(x2-t,y2),
∴x1y2-x2y1=t(y1-y2),
∵(x1y2-x2y1)t(y1-y2)=$2{{y}_{2}}^{2}-2{{y}_{1}}^{2}$=2(y1-y2)(y1+y2),
若y1=y2,则k1=k2=0,
若y1≠y2,则x1y2+x2y1=$\frac{2}{t}({y}_{1}+{y}_{2})$,
∴k1+k2=$\frac{{y}_{1}}{{x}_{1}-\frac{2}{t}}$+$\frac{{y}_{2}}{{x}_{2}-\frac{2}{t}}$=$\frac{{x}_{1}{y}_{2}+{x}_{2}{y}_{1}-\frac{2}{t}({y}_{1}+{y}_{2})}{({x}_{1}-\frac{2}{t})({x}_{2}-\frac{2}{t})}$=0,
∵点B关于x轴对称的点B′(-x2,y2),∴${k}_{QA}={k}_{Q{B}^{'}}$,∴Q,A,B三点共线,
∴$\frac{QA}{QB}$=$\frac{QA}{Q{B}^{'}}$=$\frac{|{y}_{1}|}{|{y}_{2}|}$=$\frac{PA}{PB}$,
∴对任意直线l,均有$\frac{QA}{QB}=\frac{PA}{PB}$.
点评 本题考查椭圆方程的求法,考查两直线斜率之和为定值的证明,考查满足条件的点的坐标的求法,是中档题,解题时要认真审题,注意椭圆性质、待定系数法的合理运用.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:解答题
 某小学五年级一次考试中,五名同学的语文、英语成绩如表所示:
某小学五年级一次考试中,五名同学的语文、英语成绩如表所示:| 学生 | A1 | A2 | A3 | A4 | A5 |
| 语文(x分) | 89 | 91 | 93 | 95 | 97 |
| 英语(y分) | 87 | 89 | 89 | 92 | 93 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 编号 | 1 | 2 | 3 | 4 | 5 |
| x | 169 | 178 | 166 | 175 | 180 |
| y | 75 | 80 | 77 | 70 | 81 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 13 | B. | $\sqrt{37}$ | C. | $\sqrt{13}$ | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
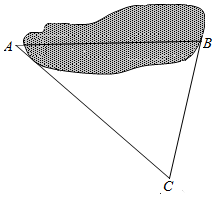 A,B两地之间隔着一个水塘(如图),现选择另一点C,测得CA=10$\sqrt{7}$km,CB=10km,∠CBA=60°.
A,B两地之间隔着一个水塘(如图),现选择另一点C,测得CA=10$\sqrt{7}$km,CB=10km,∠CBA=60°.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
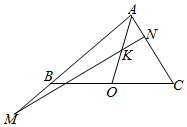 如图所示,在△ABC中,AO是BC边上的中线,K为AO上一点,且$\overrightarrow{AO}$=2$\overrightarrow{AK}$,过点K的直线分别交直线AB、AC于不同的两点M,N,若$\overrightarrow{AB}$=m$\overrightarrow{AM}$,$\overrightarrow{AC}$=n$\overrightarrow{AN}$,则m+n=4.
如图所示,在△ABC中,AO是BC边上的中线,K为AO上一点,且$\overrightarrow{AO}$=2$\overrightarrow{AK}$,过点K的直线分别交直线AB、AC于不同的两点M,N,若$\overrightarrow{AB}$=m$\overrightarrow{AM}$,$\overrightarrow{AC}$=n$\overrightarrow{AN}$,则m+n=4.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$\frac{3}{5}$,4] | B. | [$\frac{4}{5}$,5] | C. | [$\frac{4}{5}$,6] | D. | [$\frac{3}{5}$,5] |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com