
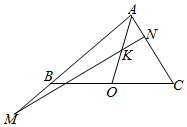
 如图所示,在△ABC中,AO是BC边上的中线,K为AO上一点,且$\overrightarrow{AO}$=2$\overrightarrow{AK}$,过点K的直线分别交直线AB、AC于不同的两点M,N,若$\overrightarrow{AB}$=m$\overrightarrow{AM}$,$\overrightarrow{AC}$=n$\overrightarrow{AN}$,则m+n=4.
如图所示,在△ABC中,AO是BC边上的中线,K为AO上一点,且$\overrightarrow{AO}$=2$\overrightarrow{AK}$,过点K的直线分别交直线AB、AC于不同的两点M,N,若$\overrightarrow{AB}$=m$\overrightarrow{AM}$,$\overrightarrow{AC}$=n$\overrightarrow{AN}$,则m+n=4. 分析 可由M,K,N三点共线得到$\overrightarrow{AK}=(1-λ)\overrightarrow{AM}+λ\overrightarrow{AN}$,而由AO为BC边上的中线便可得到$\overrightarrow{AO}=\frac{1}{2}(\overrightarrow{AB}+\overrightarrow{AC})$,从而便可根据条件得出$\overrightarrow{AK}=\frac{m}{4}\overrightarrow{AM}+\frac{n}{4}\overrightarrow{AN}$,这样由平面向量基本定理便可得出m,n和λ的关系,消去λ便可求出m+n的值.
解答 解:M,K,N三点共线;
∴$\overrightarrow{AK}=(1-λ)\overrightarrow{AM}+λ\overrightarrow{AN}$;
AO是BC边上的中线;
∴$\overrightarrow{AO}=\frac{1}{2}(\overrightarrow{AB}+\overrightarrow{AC})$;
又$\overrightarrow{AO}=2\overrightarrow{AK},\overrightarrow{AB}=m\overrightarrow{AM},\overrightarrow{AC}=n\overrightarrow{AN}$;
∴$2\overrightarrow{AK}=\frac{m}{2}\overrightarrow{AM}+\frac{n}{2}\overrightarrow{AN}$;
∴$\overrightarrow{AK}=\frac{m}{4}\overrightarrow{AM}+\frac{n}{4}\overrightarrow{AN}$;
∴由平面向量基本定理得,$\left\{\begin{array}{l}{1-λ=\frac{m}{4}}\\{λ=\frac{n}{4}}\end{array}\right.$;
∴$1=\frac{m+n}{4}$;
∴m+n=4.
故答案为:4.
点评 考查A,B,C三点共线时,便有$\overrightarrow{OB}=(1-λ)\overrightarrow{OA}+λ\overrightarrow{OC}$,向量加法的平行四边形法则,向量的数乘运算,以及平面向量基本定理.


 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{{π}^{2}}{4}$-1 | B. | $\frac{3{π}^{2}}{16}$-1 | C. | $\frac{3{π}^{2}}{4}$-1 | D. | $\frac{{π}^{2}}{8}$-1 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的一个焦点是($\sqrt{3}$,0),点P($\sqrt{3}$,$\frac{1}{2}$)在椭圆上,O为坐标原点,当直线l:y=kx+m(m≠0)与椭圆C相交于A、B两点时,对满足条件的任意m的值,都有|OA|2+|OB|2=5.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)的一个焦点是($\sqrt{3}$,0),点P($\sqrt{3}$,$\frac{1}{2}$)在椭圆上,O为坐标原点,当直线l:y=kx+m(m≠0)与椭圆C相交于A、B两点时,对满足条件的任意m的值,都有|OA|2+|OB|2=5.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com