已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1的一个焦点是.点P($\sqrt{3}$.$\frac{1}{2}$)在椭圆上.O为坐标原点.当直线l:y=kx+m与椭圆C相交于A.B两点时.对满足条件的任意m的值.都有|OA|2+|OB|2=5．(1)求椭圆C的方程．(2)求△AOB的面积S的最大值.并求� 题目和参考答案——青夏教育精英家教网—

3．

已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）的一个焦点是（$\sqrt{3}$，0），点P（$\sqrt{3}$，$\frac{1}{2}$）在椭圆上，O为坐标原点，当直线l：y=kx+m（m≠0）与椭圆C相交于A、B两点时，对满足条件的任意m的值，都有|OA|²+|OB|²=5．
（1）求椭圆C的方程．
（2）求△AOB的面积S的最大值，并求出相应m的值．

分析（1）由题意可得c=$\sqrt{3}$，即a²-b²=3，将P的坐标代入椭圆方程，解方程可得a，b，进而得到椭圆方程；
（2）将直线方程代入椭圆方程，运用韦达定理和弦长公式，以及点到直线的距离公式，求得三角形的面积，由基本不等式可得最大值，及等号成立的条件，代入判别式和条件，检验即可得到所求值．

解答解：（1）由题意可得c=$\sqrt{3}$，即a²-b²=3，
P的坐标代入椭圆方程可得$\frac{3}{{a}^{2}}$+$\frac{1}{4{b}^{2}}$=1，
解得a=2，b=1，
即有椭圆的方程为$\frac{{x}^{2}}{4}$+y²=1；
（2）设直线AB的方程为y=kx+m，m≠0，
O到直线AB的距离为d=$\frac{|m|}{\sqrt{1+{k}^{2}}}$，
将直线y=kx+m代入椭圆方程，可得
（1+4k²）x²+8kmx+4m²-4=0，
由判别式64k²m²-4（1+4k²）（4m²-4）＞0，
化简得1+4k²-m²＞0，
设A（x₁，y₁），B（x₂，y₂），可得
x₁+x₂=-$\frac{8km}{1+4{k}^{2}}$，x₁x₂=$\frac{4{m}^{2}-4}{1+4{k}^{2}}$，
|MN|=$\sqrt{1+{k}^{2}}$•$\sqrt{\frac{64{k}^{2}{m}^{2}}{（1+4{k}^{2}）^{2}}-\frac{16{m}^{2}-16}{1+4{k}^{2}}}$=$\sqrt{1+{k}^{2}}$•$\frac{4\sqrt{1+4{k}^{2}-{m}^{2}}}{1+4{k}^{2}}$，
即有△MNP面积为$\frac{1}{2}$d•|AB|=2•|m|•$\frac{\sqrt{1+4{k}^{2}-{m}^{2}}}{1+4{k}^{2}}$=2•$\frac{\sqrt{{m}^{2}（1+4{k}^{2}-{m}^{2}）}}{1+4{k}^{2}}$≤2•$\frac{{m}^{2}+1+4{k}^{2}-{m}^{2}}{2}$•$\frac{1}{1+4{k}^{2}}$=1，
当且仅当m²=1+4k²-m²，即1+4k²=2m²取得最大值1，
由1+4k²=2m²代入判别式大于0成立；
可得x₁+x₂=-$\frac{4k}{m}$，x₁x₂=2-$\frac{2}{{m}^{2}}$，
由y₁=kx₁+m，y₂=kx₂+m，
可得|OA|²+|OB|²=x₁²+y₁²+x₂²+y₂²=（1+k²）[（x₁+x₂）²-2x₁x₂]+2m²+2km（x₁+x₂）=5，
即有（1+k²）[（-$\frac{4k}{m}$）²-2（2-$\frac{2}{{m}^{2}}$）]+2m²+2km（-$\frac{4k}{m}$）=4-4k²+2m²=4+1=5．
则1+4k²=2m²恒成立．
故当m=±$\sqrt{\frac{1+4{k}^{2}}{2}}$时，△OAB的面积取得最大值1．

点评本题考查椭圆的方程的求法，注意点满足椭圆方程，考查直线和椭圆方程联立，运用韦达定理和弦长公式，以及点到直线的距离公式，基本不等式的运用：求最值，考查化简整理的运算能力，属于中档题．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源： 题型：解答题

13．某人经营一个抽奖游戏，顾客花费2元钱可购买一次游戏机会，每次游戏中，顾客从装有1个黑球，3个红球，6个白球的不透明袋子中依次不放回地摸出3个球（除颜色外其他都相同），根据摸出的球的颜色情况进行兑奖．顾客获得一等奖、二等奖、三等奖、四等奖时分别可领取奖金a元、10元、5元、2元．若经营者将顾客摸出的球的颜色情况分成以下类别：A：1个黑球2个红球；B：3个红球；C：恰有1个白球；D：恰有2个白球；E：3个白球．且经营者计划将五种类别按照发生机会从小到大的顺序分别对应中一等奖、中二等奖、中三等奖、中四等奖、不中奖五个层次．
（Ⅰ）请写出一至四等将分别对应的类别（写出字母即可）；
（Ⅱ）若经营者不打算在这个游戏的经营中亏本，求a的最大值；
（Ⅲ）若a=50，当顾客摸出的第一个球是红球时，求他领取的奖金的平均值．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

14．过点P（1，-1）作圆x²+y²-2x-2y+1=0的切线，求切线方程．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

11．2015年12月27日全国人大常委会表决通过了人口与计划生育法修正案全面二孩定于20I6年1月1日起正式实施，为了解适龄民众对放开生育二胎政策的态度，某机构从某市选取70后和80后作为调查对象．随机调查了100位，得到数据如下表：

	生二孩	不生二孩	合计
70后	30	15	45
80后	45	10	55
合计	75	25	100

（1）以这100个人的样本数据估计该市的总体数据，且以频率估计概率，若以该市70后公民中随机抽取3位，记其中生二孩的人数为X，求随机变量X的分布列和数学期望．
（2）根据调查数据，是否在犯错误的概率不超过0.1的前提下（有90%以上自把握）认为“生二孩与年龄有关”？并说明理由．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

18．平面向量$\overrightarrow{a}$与$\overrightarrow{b}$夹角为$\frac{2π}{3}$，$\overrightarrow a=（{3，0}），|{\overrightarrow b}|=2$，则$|{\overrightarrow a+2\overrightarrow b}|$等于（　　）

A．

B．

$\sqrt{37}$

C．

$\sqrt{13}$

D．

查看答案和解析>>

科目：高中数学 来源： 题型：解答题

8．已知x₁，x₂是关于x的一元二次方程4kx²-4kx+k+1=0的两个实数根．
（1）求实数k，使（2x₁-x₂）（x₁-2x₂）=-$\frac{3}{2}$；
（2）求使$\frac{{x}_{1}}{{x}_{2}}$+$\frac{{x}_{2}}{{x}_{1}}$-2的值为整数的实数k的整数值；
（3）若k=-2，λ=$\frac{{x}_{1}}{{x}_{2}}$，试求λ的值．

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

15．

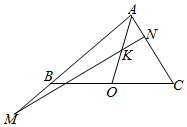如图所示，在△ABC中，AO是BC边上的中线，K为AO上一点，且$\overrightarrow{AO}$=2$\overrightarrow{AK}$，过点K的直线分别交直线AB、AC于不同的两点M，N，若$\overrightarrow{AB}$=m$\overrightarrow{AM}$，$\overrightarrow{AC}$=n$\overrightarrow{AN}$，则m+n=4．

查看答案和解析>>

科目：高中数学 来源： 题型：填空题

12．已知sin（$\frac{π}{5}$-α）=$\frac{1}{3}$，则cos（2α+$\frac{3π}{5}$）=-$\frac{7}{9}$．

查看答案和解析>>

科目：高中数学 来源： 题型：选择题

13．函数y=$\left\{\begin{array}{l}{2x}&{x≥0}\\{-{x}^{2}}&{x＜0}\end{array}\right.$的反函数是（　　）

	A．	y=$\left\{\begin{array}{l}{\frac{x}{2}}&{x≥0}\\{\sqrt{-x}}&{x＜0}\end{array}\right.$		B．	y=$\left\{\begin{array}{l}{\frac{x}{2}}&{x≥0}\\{-\sqrt{-x}}&{x＜0}\end{array}\right.$
	C．	y=$\left\{\begin{array}{l}{2x}&{x≥0}\\{\sqrt{-x}}&{x＜0}\end{array}\right.$		D．	y=$\left\{\begin{array}{l}{2x}&{x≥0}\\{-\sqrt{-x}}&{x＜0}\end{array}\right.$

查看答案和解析>>

同步练习册答案

练习册

高中

初中

小学