考点:直线与平面垂直的性质,棱柱的结构特征,棱柱、棱锥、棱台的体积,空间中直线与直线之间的位置关系
专题:转化思想,空间位置关系与距离
分析:(1)由已知条件推导出BC⊥CD,BC⊥CC1,从而得到BC⊥平面DCC1D1,由此能够证明BC⊥D1E.
(2)DD1∥B1BCC1,三棱锥D1-B1CB的体积等于三棱锥D-B1CB的体积,就是三棱锥B1-DCB的体积,B1到底面DCB的距离就是D1E,求出底面面积以及高,即可求出体积.
解答:
(1)证明:∵底面ABCD和侧面BCC
1B
1是矩形,
∴BC⊥CD,BC⊥CC
1,
又∵CD∩CC
1=C,
∴BC⊥平面DCC
1D
1,
∵D
1E?平面DCC
1D
1,∴BC⊥D
1E.
(2)在四棱柱ABCD-A
1B
1C
1D
1中,DD
1∥B
1BCC
1,
∴三棱锥D
1-B
1CB的体积等于三棱锥D-B
1CB的体积,
就是三棱锥B
1-DCB的体积,B
1到底面DCB的距离就是D
1E,
在四棱柱ABCD-A
1B
1C
1D
1中,底面ABCD和侧面BCC
1B
1都是矩形,E是CD的中点,
D
1E⊥CD,AB=2BC=2.
AA
1=
,
∴D
1E=
=
=1.
所求体积:V=
S△DCB•D1E=
××2×2×1=
点评:本题考查异面直线垂直的证明,考查直线与平面平行的性质,几何体的体积的求法,考查线段长的求法,解题时要认真审题.考查转化思想.

 如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD和侧面BCC1B1都是矩形,E是CD的中点,D1E⊥CD,AB=2BC=2.
如图,在四棱柱ABCD-A1B1C1D1中,底面ABCD和侧面BCC1B1都是矩形,E是CD的中点,D1E⊥CD,AB=2BC=2.

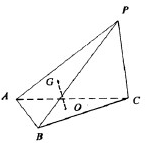 如图,在三棱锥P-ABC中,△ABC是边长等于2的正三角形,且∠PCA=∠PCB.
如图,在三棱锥P-ABC中,△ABC是边长等于2的正三角形,且∠PCA=∠PCB.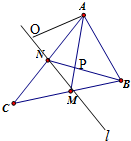 在△ABC中,已知AB=2,AC=6,∠BAC=60°,中线AM、BN交于点P,设
在△ABC中,已知AB=2,AC=6,∠BAC=60°,中线AM、BN交于点P,设