
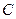 :
: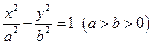 和圆
和圆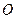 :
: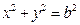 (其中原点
(其中原点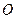 为圆心),过双曲线
为圆心),过双曲线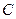 上一点
上一点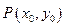 引圆
引圆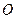 的两条切线,切点分别为
的两条切线,切点分别为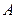 、
、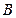 .
.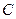 上存在点
上存在点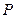 ,使得
,使得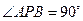 ,求双曲线离心率
,求双曲线离心率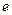 的取值范围;
的取值范围; 的方程;
的方程;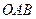 面积的最大值.
面积的最大值.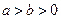 ,所以
,所以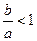 ,所以
,所以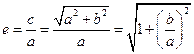
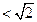 .…………………1分
.…………………1分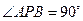 及圆的性质,可知四边形
及圆的性质,可知四边形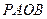 是正方形,所以
是正方形,所以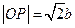 .
.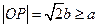 ,所以
,所以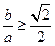 ,所以
,所以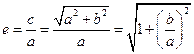
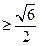 .……………3分
.……………3分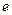 的取值范围为
的取值范围为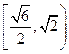 .…………………………………………………………4分
.…………………………………………………………4分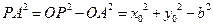 ,
,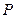 为圆心,
为圆心,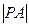 为半径的圆
为半径的圆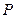 的方程为
的方程为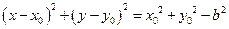 .………5分
.………5分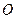 与圆
与圆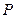 两圆的公共弦所在的直线即为直线
两圆的公共弦所在的直线即为直线 ,……………………………………………6分
,……………………………………………6分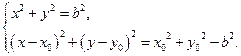 ………………………………………………7分
………………………………………………7分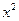 ,
,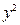 ,即得直线
,即得直线 的方程为
的方程为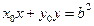 .………………………………………………8分
.………………………………………………8分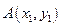
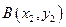 ,已知点
,已知点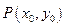 ,
,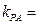
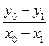 ,
,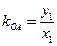
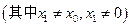 .
.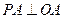 ,所以
,所以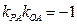 ,即
,即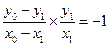 .…………………………………………5分
.…………………………………………5分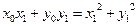 .
.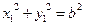 ,所以
,所以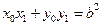 .……………………………………………………………6分
.……………………………………………………………6分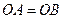 ,
,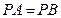 ,根据平面几何知识可知,
,根据平面几何知识可知,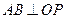 .
.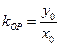 ,所以
,所以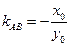 .………………………………………………………………………7分
.………………………………………………………………………7分 方程为
方程为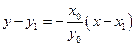 .
.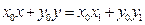 .
. 的方程为
的方程为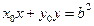 .………………………………………………………………8分
.………………………………………………………………8分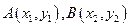 ,已知点
,已知点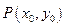 ,
,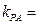
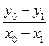 ,
,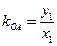
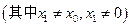 .
.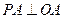 ,所以
,所以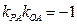 ,即
,即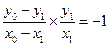 .…………………………………………5分
.…………………………………………5分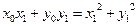 .
.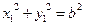 ,所以
,所以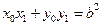 .……6分
.……6分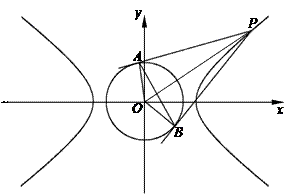
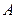 在直线
在直线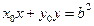 上.…………7分
上.…………7分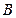 也在直线
也在直线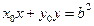 上.
上.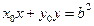 就是直线
就是直线 的方程.……8分
的方程.……8分 的方程为
的方程为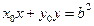 ,
,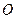 到直线
到直线 的距离为
的距离为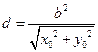 .
.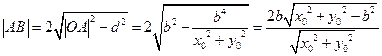 ,
,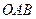 的面积
的面积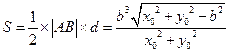 .……………………………………10分
.……………………………………10分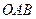 的面积
的面积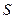 的三种方法:
的三种方法: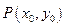 在双曲线
在双曲线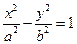 上,
上,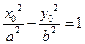 ,即
,即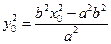
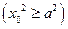 .
.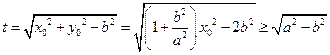 ,
,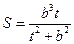 .………………………………………………………………………………………11分
.………………………………………………………………………………………11分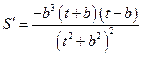 ,
,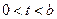 时,
时,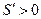 ,当
,当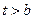 时,
时,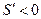 .
.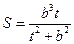 在
在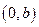 上单调递增,在
上单调递增,在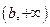 上单调递减.……………………………………12分
上单调递减.……………………………………12分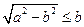 ,即
,即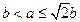 时,
时,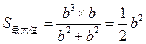 ,…………………………………13分
,…………………………………13分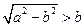 ,即
,即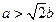 时,
时,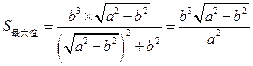 .
.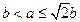 时,
时,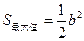 ;当
;当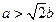 时,
时,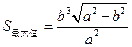 .………14分
.………14分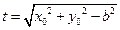 ,则
,则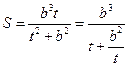 .…………………………………………11分
.…………………………………………11分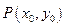 在双曲线
在双曲线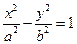 上,即
上,即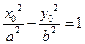 ,即
,即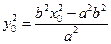
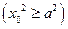 .
.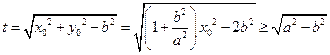 .
.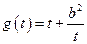 ,则
,则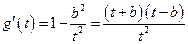 .
.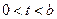 时,
时,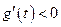 ,当
,当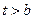 时,
时,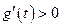 .
.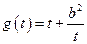 在
在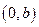 上单调递减,在
上单调递减,在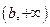 上单调递增.…………………………………12分
上单调递增.…………………………………12分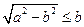 ,即
,即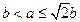 时,
时,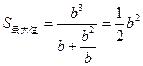 ,……………………………………13分
,……………………………………13分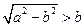 ,即
,即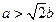 时,
时,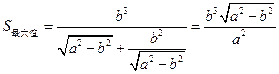 .
.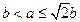 时,
时,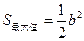 ;当
;当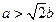 时,
时,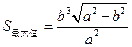 .………14分
.………14分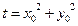 ,则
,则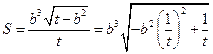 .…………………………………11分
.…………………………………11分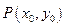 在双曲线
在双曲线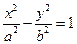 上,即
上,即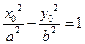 ,即
,即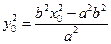
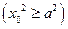 .
.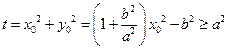 .
.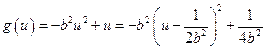 ,
,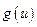 在
在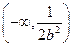 上单调递增,在
上单调递增,在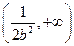 上单调递减.………………………………12分
上单调递减.………………………………12分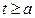 ,所以
,所以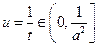 ,
,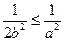 ,即
,即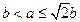 时,
时,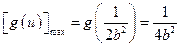 ,此时
,此时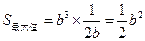 .
.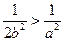 ,即
,即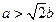 时,
时,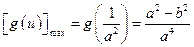 ,此时
,此时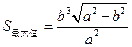 .
.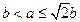 时,
时,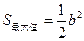 ;当
;当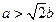 时,
时,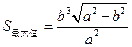 .………14分
.………14分

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:不详 题型:解答题
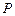 是椭圆
是椭圆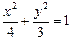 上一动点,点
上一动点,点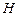 是点
是点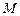 在
在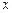 轴上的射影,坐标平面
轴上的射影,坐标平面 内动点
内动点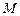 满足:
满足: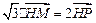 (
(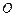 为坐标原点),设动点
为坐标原点),设动点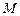 的轨迹为曲线
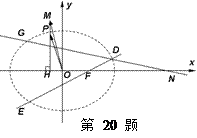
的轨迹为曲线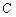 .
.
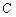 的方程并画出草图;
的方程并画出草图;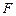 的直线
的直线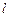 交曲线
交曲线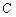 于
于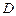 ,
,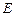 两点,且
两点,且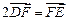 ,点
,点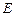 关于
关于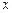 轴的对称点为
轴的对称点为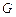 ,求直线
,求直线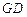 的方程.
的方程.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
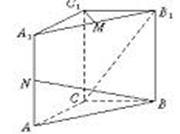
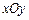 中,
中,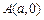
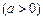 ,
,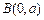 ,
,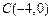 ,
,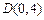 ,设
,设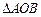 的外接圆圆心为E.
的外接圆圆心为E.
 (1)若⊙E与直线CD相切,求实数a的值;
(1)若⊙E与直线CD相切,求实数a的值; (2)设点
(2)设点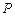 在圆
在圆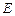 上,使
上,使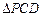 的面积等于12的点
的面积等于12的点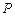 有且只有三个,试问这样的⊙E是否存在,若存在,求出⊙E的标准方程;若不存在,说明理由.
有且只有三个,试问这样的⊙E是否存在,若存在,求出⊙E的标准方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
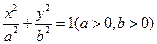 的右顶点为
的右顶点为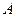 ,点
,点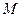 在椭圆上,且它的横坐标为1,点
在椭圆上,且它的横坐标为1,点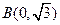 ,且
,且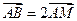 .
.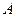 的直线
的直线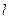 与椭圆交于另一点
与椭圆交于另一点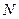 ,若线段
,若线段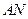 的垂直平分线经过点
的垂直平分线经过点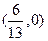 ,求直线
,求直线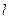 的方程.
的方程.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
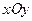 中,已知动点
中,已知动点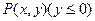 到点
到点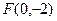 的距离为
的距离为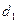 ,到
,到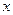 轴的距离为
轴的距离为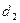 ,且
,且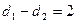 .
.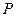 的轨迹
的轨迹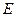 的方程;
的方程;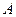 、
、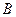 是(I)中
是(I)中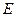 上的两点,
上的两点,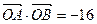 ,过
,过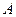 、
、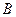 分别作直线
分别作直线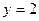 的垂线,垂足分别为
的垂线,垂足分别为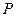 、
、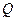 .证明:直线
.证明:直线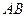 过定点
过定点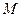 ,且
,且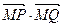 为定值.
为定值.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
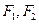 ,离心率为
,离心率为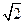 ,且过点
,且过点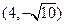 ,
,
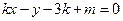 (其中
(其中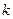 为参数)所过的定点
为参数)所过的定点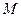 恰在双曲线上,求证:
恰在双曲线上,求证: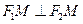 。
。查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
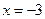 的距离小1,求点M满足的方程。
的距离小1,求点M满足的方程。查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com