
分析 由条件利用二项式展开式的通项公式求得a的值,再利用积分的运算性质、法则,求得要求式子的值.
解答 解:由${(\frac{a}{{\sqrt{x}}}-x)^6}$的展开式的通项公式为Tr+1=${C}_{6}^{r}$•(-1)r•a6-r•${x}^{\frac{3r-6}{2}}$,
令$\frac{3r-6}{2}$=0,求得r=2,故常数项为$C_6^4{a^4}=15$,可得a=1,
因此原式为$\int_{-1}^1{({x^2}+x+\sqrt{4-{x^2}})}dx=2\int_0^1{({x^2}+\sqrt{4-{x^2}})}dx=2(\int_0^1{x^2}dx+\int_0^1{\sqrt{4-{x^2}}}dx)$
=$2(\frac{1}{3}+\frac{{π•{2^2}}}{12}+\frac{1}{2}×1×\sqrt{3})=\frac{2}{3}+\frac{2π}{3}+\sqrt{3}$,
故答案为:$\frac{2}{3}+\frac{2π}{3}+\sqrt{3}$.
点评 本题主要考查二项式定理的应用,二项式展开式的通项公式,积分的运算,是一道中档的常规问题


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
 如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各条棱中,最长的棱的长度为( )
如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的各条棱中,最长的棱的长度为( )| A. | $2\sqrt{3}$ | B. | $2\sqrt{2}$ | C. | $\sqrt{10}$ | D. | $\sqrt{13}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | rl=r2 | B. | r1>r2>0 | C. | 0<r1<r2 | D. | r1<0<r2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1-i}{2}$ | B. | $\frac{1+i}{2}$ | C. | 1-i | D. | 1+i |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|2<x<3} | B. | {x|-2<x<0} | C. | {x|0<x<2} | D. | {x|-2<x<3} |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 关于点($\frac{π}{8}$,0)对称 | B. | 关于直线x=$\frac{π}{8}$对称 | ||
| C. | 关于点(-$\frac{π}{4}$,0)对称 | D. | 关于直线x=-$\frac{π}{4}$对称 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
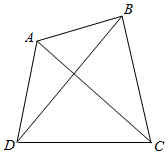 为了测量河对岸两点A,B之间的距离,在河岸的这边选取点C、D,测得∠ADC=75°,∠BDC=60°,∠ACD=45°,∠BCD=75°,CD=20$\sqrt{3}$m,设A,B,C,D在同一平面内,求A,B之间的距离.
为了测量河对岸两点A,B之间的距离,在河岸的这边选取点C、D,测得∠ADC=75°,∠BDC=60°,∠ACD=45°,∠BCD=75°,CD=20$\sqrt{3}$m,设A,B,C,D在同一平面内,求A,B之间的距离.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1+i}{2}$ | B. | $\frac{1-i}{2}$ | C. | $\frac{-1-i}{2}$ | D. | $\frac{-1+i}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com