
分析 由于函数f(x)是分段函数,且对任意的非零实数x1,存在唯一的非零实数x2(x2≠x1),使得f(x2)=f(x1)成立,得到x=0时,f(x)=k(1-a2),进而得到,关于a的方程(3-a)2=k(1-a2)有实数解,即得△≥0,解出k即可.
解答 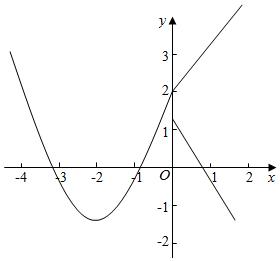 解:由分段函数的表达式当x=0时,f(x)=k(1-a2),
解:由分段函数的表达式当x=0时,f(x)=k(1-a2),
又由对任意的非零实数x1,存在唯一的非零实数x2(x2≠x1),使得f(x2)=f(x1)成立,
∴函数必须为连续函数,即在x=0附近的左右两侧函数值相等,
∴k≠0,且(3-a)2=k(1-a2),即(k+1)a2-6a+9-k=0有实数解,
所以△=62-4(k+1)(9-k)≥0,解得k≤0或k≥8,
又∵k≠0,
∴k的取值范围为k<0或k≥8,
故答案为:k<0或k≥8.
点评 本题主要考查分段函数的应用,结合一元二次函数的性质是解决本题的关键.综合性较强,难度较大.注意利用数形结合进行求解.


 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 某几何体的三视图如图所示(单位:cm),则该几何体的体积是( )cm3.
某几何体的三视图如图所示(单位:cm),则该几何体的体积是( )cm3.| A. | 1+2π | B. | 1+$\frac{4π}{3}$ | C. | 1+$\frac{π}{2}$ | D. | 1+$\frac{π}{6}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{3}{2}$π | B. | π+1 | C. | π+$\frac{1}{6}$ | D. | π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
 若某空间几何体的三视图如图所示,根据图中数据,可得该几何体的外接球的体积是( )
若某空间几何体的三视图如图所示,根据图中数据,可得该几何体的外接球的体积是( )| A. | $\frac{{\sqrt{2}}}{3}$π | B. | $\frac{4}{3}$π | C. | $\sqrt{6}$π | D. | 8$\sqrt{6}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | {x|$\frac{1}{a}$<x<1} | B. | {x|-1<x<$\frac{1}{a}$} | C. | {x|1$<x<\frac{1}{a}$} | D. | {x|-$\frac{1}{a}$<x<-1} |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com