(1)等比数列{an}中,对任意n≥2,n∈N时都有an-1,an+1,an成等差,求公比q的值;
(2)设Sn是等比数列{an}的前n项和,当S3,S9,S6成等差时,是否有a2,a8,a5一定也成等差数列?说明理由;
(3)设等比数列{an}的公比为q,前n项和为Sn,是否存在正整数k,使Sm-k,Sm+k,Sm成等差且an-k,an+k,an也成等差,若存在,求出k与q满足的关系;若不存在,请说明理由.
解:(1)当n≥2,n∈N时,a
n-1,a
n+1,a
n成等差,故有a
n-1+a
n=2a
n+1 ,1+q=2q
2.
解得q=1或
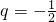
.…5分
(2)当q=1时S
n=na
1,显然3a
1,9a
1,6a
1不是等差数列,
所以q≠1,
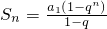
.由S
3,S
9,S
6成等差数列得

,
化简可得q
3+q
6=2q
9,求得
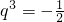
或q
3=1(不合题意)所以
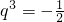
.
所以 1+q
3=2q
6,
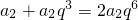
,a
2+a
5=2a
8.
即一定有a
2,a
8,a
5成等差数列.…11分
(3)假设存在正整数k,使S
m-k,S
m+k,S
m成等差且a
n-k,a
n+k,a
n也成等差.
当q=1时S
n=na
1,显然(m-k)a
1,(m+k)a
1,ma
1不是等差数列,
所以q≠1,
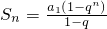
. …13分
由S
m-k,S
m+k,S
m成等差数列得

,
即 q
m-k+q
m=2q
m+k ,即 1+q
k=2q
2k. 解得

,或q
k=1.…16分
当k为偶数时,q=-1,则有S
m-k=S
m+k=S
m且a
n-k=a
n+k=a
n.
当k为奇数时,

;∴1+q
k=2q
2k,∴
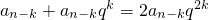
,
∴a
n-k+a
n=2a
n+k.
综上所述,存在正整数k(k<m,k<n)满足题设,当k为偶数时,q=-1;当k为奇数时,

.…18分.
分析:(1)由题意可得 a
n-1+a
n=2a
n+1 ,1+q=2q
2 ,由此求得公比q的值.
(2)当q=1时S
n=na
1,显然3a
1,9a
1,6a
1不是等差数列,所以q≠1,由S
3,S
9,S
6成等差数列化简可得
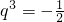
,
可得
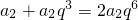
,a
2+a
5=2a
8,从而得出结论.
(3)当q=1时,检验不满足条件.所以q≠1,
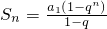
.由S
m-k,S
m+k,S
m成等差数列化简可得得

,或q
k=1.分k为偶数、k为奇数两种情况,分别求出k与q满足的关系,从而得出结论.
点评:本题主要考查等差数列的定义和性质,等比数列的通项公式,等比数列的前n项和公式,体现了分类讨论的数学思想,属于中档题.

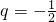 .…5分
.…5分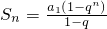 .由S3,S9,S6成等差数列得
.由S3,S9,S6成等差数列得 ,
,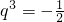 或q3=1(不合题意)所以
或q3=1(不合题意)所以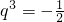 .
.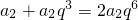 ,a2+a5=2a8.
,a2+a5=2a8.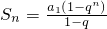 . …13分
. …13分 ,
, ,或qk=1.…16分
,或qk=1.…16分 ;∴1+qk=2q2k,∴
;∴1+qk=2q2k,∴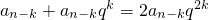 ,
, .…18分.
.…18分.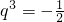 ,
,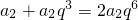 ,a2+a5=2a8,从而得出结论.
,a2+a5=2a8,从而得出结论.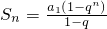 .由Sm-k,Sm+k,Sm成等差数列化简可得得
.由Sm-k,Sm+k,Sm成等差数列化简可得得  ,或qk=1.分k为偶数、k为奇数两种情况,分别求出k与q满足的关系,从而得出结论.
,或qk=1.分k为偶数、k为奇数两种情况,分别求出k与q满足的关系,从而得出结论.

 期末集结号系列答案
期末集结号系列答案