
【题目】抛物线![]() 和圆
和圆![]() ,直线
,直线![]() 与抛物线
与抛物线![]() 和圆
和圆![]() 分别交于四个点
分别交于四个点![]() (自下而上的顺序为
(自下而上的顺序为![]() ),则
),则![]() 的值为_________.
的值为_________.
 一线名师提优试卷系列答案
一线名师提优试卷系列答案科目:高中数学 来源: 题型:
【题目】已知动圆![]() 过定点
过定点![]() 且在
且在![]() 轴上截得的弦长为4。
轴上截得的弦长为4。
(1)求动圆![]() 的圆心
的圆心![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过点![]() 的动直线与曲线
的动直线与曲线![]() 交于
交于![]() 两点,点
两点,点![]() 在曲线
在曲线![]() 上,使得
上,使得![]() 的重心
的重心![]() 在
在![]() 轴上,直线
轴上,直线![]() 交
交![]() 轴于点
轴于点![]() ,且点
,且点![]() 在点
在点![]() 的右侧,记
的右侧,记![]() 的面积为
的面积为![]() 的面积为
的面积为![]() ,求
,求![]() 的最小值。
的最小值。
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知过椭圆![]() 的左焦点
的左焦点![]() ,作斜率为
,作斜率为![]() 的直线
的直线![]() ,交椭圆
,交椭圆![]() 于
于![]() 两点.
两点.
(1)若原点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,求直线
,求直线![]() 的方程;
的方程;
(2)设点![]() ,直线
,直线![]() 与椭圆
与椭圆![]() 交于另一点
交于另一点![]() ,直线
,直线![]() 与椭圆
与椭圆![]() 交于另一点
交于另一点![]() .设
.设![]() 的斜率为
的斜率为![]() ,则
,则![]() 是否为定值?若是,求出该定值;若不是,请说明理由.
是否为定值?若是,求出该定值;若不是,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 的焦距为
的焦距为![]() ,椭圆
,椭圆![]() 上任意一点到椭圆两个焦点的距离之和为6.
上任意一点到椭圆两个焦点的距离之和为6.
(Ⅰ)求椭圆![]() 的方程;
的方程;
(Ⅱ)设直线![]()
![]() 与椭圆
与椭圆![]() 交于
交于![]() 两点,点
两点,点![]() (0,1),且
(0,1),且![]() =
=![]() ,求直线
,求直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某生鲜批发店每天从蔬菜生产基地以5元/千克购进某种绿色蔬菜,售价8元/千克,若每天下午4点以前所购进的绿色蔬菜没有售完,则对未售出的绿色蔬菜降价处理,以3元/千克出售.根据经验,降价后能够把剩余蔬菜全部处理完毕,且当天不再进货.该生鲜批发店整理了过往30天(每天下午4点以前)这种绿色蔬菜的日销售量(单位:千克)得到如下统计数据(视频率为概率)(注:x,y∈N*)
每天下午4点前销售量 | 350 | 400 | 450 | 500 | 550 |
天数 | 3 | 9 | x | y | 2 |
(1)求在未来3天中,至少有1天下午4点前的销售量不少于450千克的概率.
(2)若该生鲜批发店以当天利润期望值为决策依据,当购进450千克比购进500千克的利润期望值大时,求x的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(x﹣2)ex﹣![]() +
+![]() x,其中
x,其中![]() ∈R,e是自然对数的底数.
∈R,e是自然对数的底数.
(1)当![]() >0时,讨论函数f(x)在(1,+∞)上的单调性;
>0时,讨论函数f(x)在(1,+∞)上的单调性;
(2)若函数g(x)=f![]() (x)+2﹣
(x)+2﹣![]() ,证明:使g(x)≥0在
,证明:使g(x)≥0在![]() 上恒成立的实数a能取到的最大整数值为1.
上恒成立的实数a能取到的最大整数值为1.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() ,其图象关于直线
,其图象关于直线![]() 对称,为了得到函数
对称,为了得到函数![]() 的图象,只需将函数
的图象,只需将函数![]() 的图象上的所有点( )
的图象上的所有点( )
A.先向左平移![]() 个单位长度,再把所得各点横坐标伸长为原来的2倍,纵坐标保持不变
个单位长度,再把所得各点横坐标伸长为原来的2倍,纵坐标保持不变
B.先向右平移![]() 个单位长度,再把所得各点横坐标缩短为原来的
个单位长度,再把所得各点横坐标缩短为原来的![]() ,纵坐标保持不变
,纵坐标保持不变
C.先向右平移![]() 个单位长度,再把所得各点横坐标伸长为原来的2倍,纵坐标保持不变
个单位长度,再把所得各点横坐标伸长为原来的2倍,纵坐标保持不变
D.先向左平移![]() 个单位长度,再把所得各点横坐标缩短为原来的
个单位长度,再把所得各点横坐标缩短为原来的![]() ,纵坐标保持不变
,纵坐标保持不变
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,射线![]() 和
和![]() 均为笔直的公路,扇形
均为笔直的公路,扇形![]() 区域(含边界)是一蔬菜种植园,其中
区域(含边界)是一蔬菜种植园,其中![]() 、
、![]() 分别在射线
分别在射线![]() 和
和![]() 上.经测量得,扇形
上.经测量得,扇形![]() 的圆心角(即
的圆心角(即![]() )为
)为![]() 、半径为1千米.为了方便菜农经营,打算在扇形
、半径为1千米.为了方便菜农经营,打算在扇形![]() 区域外修建一条公路
区域外修建一条公路![]() ,分别与射线
,分别与射线![]() 、
、![]() 交于
交于![]() 、
、![]() 两点,并要求
两点,并要求![]() 与扇形弧
与扇形弧![]() 相切于点
相切于点![]() .设
.设![]() (单位:弧度),假设所有公路的宽度均忽略不计.
(单位:弧度),假设所有公路的宽度均忽略不计.
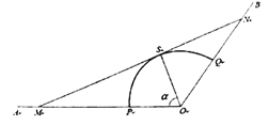
(1)试将公路![]() 的长度表示为
的长度表示为![]() 的函数,并写出
的函数,并写出![]() 的取值范围;
的取值范围;
(2)试确定![]() 的值,使得公路
的值,使得公路![]() 的长度最小,并求出其最小值.
的长度最小,并求出其最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某地拟建造一座体育馆,其设计方案侧面的外轮廓线如图所示:曲线![]() 是以点
是以点![]() 为圆心的圆的一部分,其中
为圆心的圆的一部分,其中![]()
![]() ,
,![]() 是圆的切线,且
是圆的切线,且![]() ,曲线
,曲线![]() 是抛物线
是抛物线![]()
![]() 的一部分,
的一部分,![]() ,且
,且![]() 恰好等于圆
恰好等于圆![]() 的半径.
的半径.
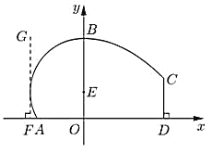
(1)若![]() 米,
米,![]() 米,求
米,求![]() 与
与![]() 的值;
的值;
(2)若体育馆侧面的最大宽度![]() 不超过75米,求
不超过75米,求![]() 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com