
| A. | -1 | B. | $-\frac{{\sqrt{3}}}{2}$ | C. | $-\sqrt{3}$ | D. | 1 |
分析 由条件利用正弦函数的定义域和值域,求得函数f(x)=2sin(2x-$\frac{π}{3}$)在区间[0,$\frac{π}{4}$]上的最小值.
解答 解:在区间[0,$\frac{π}{4}$]上,2x-$\frac{π}{3}$∈[-$\frac{π}{3}$,$\frac{π}{6}$],
故函数f(x)=2sin(2x-$\frac{π}{3}$)在区间[0,$\frac{π}{4}$]上单调递增,
故当2x-$\frac{π}{3}$=-$\frac{π}{3}$时,函数取得最小值为2sin(-$\frac{π}{3}$)=-2sin$\frac{π}{3}$=-$\sqrt{3}$,
故选:C.
点评 本题主要考查正弦函数的定义域和值域,正弦函数的单调性,属于基础题.


科目:高中数学 来源: 题型:选择题

| A. | 2016×22015 | B. | 2016×22014 | C. | 2017×22015 | D. | 2017×22014 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 长度相等的向量叫相等向量 | |
| B. | 零向量的长度为零 | |
| C. | 共线向量是在一条直线上的向量 | |
| D. | 平行向量就是向量所在的直线平行的向量 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{\sqrt{6}-\sqrt{2}}{2}$ | B. | $\frac{\sqrt{6}+\sqrt{2}}{2}$ | C. | $\frac{2+\sqrt{3}}{4}$ | D. | $\frac{2-\sqrt{3}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(sinx)>f(cosx) | B. | f($\frac{{x}^{2}+1}{2}$)>f(x) | ||
| C. | f($\frac{1}{{3}^{x}+1}$)≥f($\frac{1}{{2}^{x}+1}$) | D. | f($\frac{1}{{3}^{x}+{3}^{-x}}$)≥f($\frac{1}{{2}^{x}+{2}^{-x}}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,AF、DE分别是⊙O、⊙O1的直径,AD与两圆所在的平面均垂直,AD=8,BC是⊙O的直径,AB=AC=6,OE∥AD.
如图所示,AF、DE分别是⊙O、⊙O1的直径,AD与两圆所在的平面均垂直,AD=8,BC是⊙O的直径,AB=AC=6,OE∥AD.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
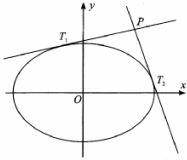 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1的短轴长为2,离心率$\frac{\sqrt{2}}{2}$.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1的短轴长为2,离心率$\frac{\sqrt{2}}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | bn=2n-1 | B. | bn=3n-1 | C. | bn=2n-2 | D. | bn=3n-2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com