
分析 由泊松分布,求出 E(ξi),D(ξi),由Z=$\sum_{i=1}^{50}$Xi,求出EZ,DZ;
根据中心极限定理知Z~N(1.5,1.5),求出P(Z≥3)的值.
解答 解:由泊松分布知,
E(ξi)=λ=0.03,D(ξi)=λ=0.03=σ2 (i=1,2,…,50);
由Z=$\sum_{i=1}^{50}$Xi,EZ=50×0.03=1.5,DZ=50×0.03=1.5;
根据中心极限定理知,Z~N(1.5,1.5);
P(Z≥3)=1-P(Z≤3)=1-P($\frac{Z-3}{\sqrt{1.5}}$≤$\frac{1.5-3}{\sqrt{1.5}}$)=1-Φ(-1.225)=0.8907.
点评 本题考查了相互独立的随机变量期望与方差的计算问题,也考查了泊松分布与中心极限定理的应用问题,是综合题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
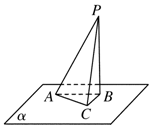 如图所示,三棱锥P-ABC的底面在平面α内,且AC⊥PC,平面PAC⊥平面PBC,点P,A,B是定点,则动点C的轨迹是( )
如图所示,三棱锥P-ABC的底面在平面α内,且AC⊥PC,平面PAC⊥平面PBC,点P,A,B是定点,则动点C的轨迹是( )| A. | 一条线段 | B. | 一条直线 | ||
| C. | 一个圆 | D. | 一个圆,但要去掉两个点 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{1}{17}$ | D. | $\frac{1}{18}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$ | B. | -2 | C. | $\frac{1}{2}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -$\frac{1}{2}$ | B. | -1 | C. | $\frac{5}{2}$ | D. | $\frac{1}{2}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com