
| A. | ±$\frac{\sqrt{3}}{3}$ | B. | ±$\sqrt{3}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\sqrt{3}$ |
分析 求出圆(x-2)2+(y-3)2=4的圆心,半径,圆心(2,3)到直线y=kx+3的距离,由此利用直线y=kx+3被圆(x-2)2+(y-3)2=4截得的弦长为$2\sqrt{3}$,由勾股定理能求出k.
解答 解:圆(x-2)2+(y-3)2=4的圆心(2,3),半径r=2,
圆心(2,3)到直线y=kx+3的距离d=$\frac{|2k|}{\sqrt{{k}^{2}+1}}$,
∵直线y=kx+3被圆(x-2)2+(y-3)2=4截得的弦长为$2\sqrt{3}$,
∴由勾股定理得${r}^{2}={d}^{2}+(\frac{2\sqrt{3}}{2})^{2}$,
即4=$\frac{4{k}^{2}}{{k}^{2}+1}$+3,
解得k=$±\frac{\sqrt{3}}{3}$.
故选:A.
点评 本题考查直线的斜率的求法,是中档题,解题时要认真审题,注意圆的性质、点到直线的距离公式的合理运用.


科目:高中数学 来源: 题型:选择题
| A. | 4π | B. | 16π | C. | $\frac{4}{3}$π | D. | $\frac{16}{3}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 2015年7月31日,国际奥委会在吉隆坡正式宣布2022年奥林匹克冬季奥运会(简称冬奥会)在北京和张家口两个城市举办.某中学为了普及奥运会知识和提高学生参加体育运动的积极性,举行了一次奥运知识竞赛.随机抽取了30名学生的成绩,绘成如图所示的茎叶图,若规定成绩在75分以上(包括75分)的学生定义为甲组,成绩在75分以下(不包括75分)定义为乙组.
2015年7月31日,国际奥委会在吉隆坡正式宣布2022年奥林匹克冬季奥运会(简称冬奥会)在北京和张家口两个城市举办.某中学为了普及奥运会知识和提高学生参加体育运动的积极性,举行了一次奥运知识竞赛.随机抽取了30名学生的成绩,绘成如图所示的茎叶图,若规定成绩在75分以上(包括75分)的学生定义为甲组,成绩在75分以下(不包括75分)定义为乙组.| P(K2>k0) | 0.100 | 0.050 | 0.010 |
| K | 2.706 | 3.841 | 6.635 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 锐角三角形 | B. | 直角三角形 | C. | 钝角三角形 | D. | 不存在 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 在三棱锥P-ABC中,平面PAC⊥平面ABC,△PAC为等腰直角三角形,PA⊥PC,AC⊥BC,BC=2AC=4,M为AB的中点.
在三棱锥P-ABC中,平面PAC⊥平面ABC,△PAC为等腰直角三角形,PA⊥PC,AC⊥BC,BC=2AC=4,M为AB的中点.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图所示,四棱锥P-ABCD的底面是梯形,且AB∥CD,AB⊥平面PAD,E是PB中点,CD=PD=AD=$\frac{1}{2}$AB.
如图所示,四棱锥P-ABCD的底面是梯形,且AB∥CD,AB⊥平面PAD,E是PB中点,CD=PD=AD=$\frac{1}{2}$AB.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
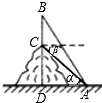 如图,山顶上有一座铁塔,在地面上一点A处测得塔顶B处的仰角α=60°,在山顶C处测得A点的俯角β=45°,已知塔高BC为50m,则山高CD等于25$({\sqrt{3}+1})$m.
如图,山顶上有一座铁塔,在地面上一点A处测得塔顶B处的仰角α=60°,在山顶C处测得A点的俯角β=45°,已知塔高BC为50m,则山高CD等于25$({\sqrt{3}+1})$m.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com