
 在三棱锥P-ABC中,平面PAC⊥平面ABC,△PAC为等腰直角三角形,PA⊥PC,AC⊥BC,BC=2AC=4,M为AB的中点.
在三棱锥P-ABC中,平面PAC⊥平面ABC,△PAC为等腰直角三角形,PA⊥PC,AC⊥BC,BC=2AC=4,M为AB的中点.分析 (I)取AC中点O,连接OP,OM,可证AC⊥平面POM,故而AC⊥PM;
(II)以O为原点建立坐标系,求出$\overrightarrow{PC}$与平面PAB的法向量$\overrightarrow{n}$的坐标,于是PC与平面PAB所成角的正弦值为|cos<$\overrightarrow{PC},\overrightarrow{n}$>|;
(III)设$\overrightarrow{PN}=λ\overrightarrow{PB}$,用λ表示出$\overrightarrow{CN}$的坐标,求出$\overrightarrow{CM}$,求出平面CNM的法向量$\overrightarrow{m}$,令$\overrightarrow{m}•\overrightarrow{n}$=0得出λ.
解答 证明:(I)取AC中点O,连接OP,OM.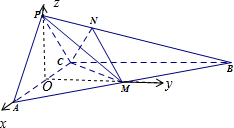 ∵PA=PC,∴PO⊥AC,
∵PA=PC,∴PO⊥AC,
∵平面PAC⊥平面ABC,平面PAC∩平面ABC=AC,
∴PO⊥平面ABC.
∵M是AB的中点,∴OM∥BC,
∵BC⊥AC,
∴OM⊥AC.又OP∩OM=O,
∴AC⊥平面POM,∵PM?平面POM,
∴AC⊥PM.
(II)以O为原点,以OA,OM,OP为坐标轴建立空间直角坐标系,如图所示:
则A(1,0,0),C(-1,0,0),P(0,0,1),B(-1,4,0).
∴$\overrightarrow{PC}$=(-1,0,-1),$\overrightarrow{AP}$=(-1,0,1),$\overrightarrow{AB}$=(-2,4,0).
设平面PAB的法向量为$\overrightarrow{n}$=(x,y,z),则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{AP}=0}\\{\overrightarrow{n}•\overrightarrow{AB}=0}\end{array}\right.$,
∴$\left\{\begin{array}{l}{-x+z=0}\\{-2x+4y=0}\end{array}\right.$,令y=1得$\overrightarrow{n}$=(2,1,2),∴cos<$\overrightarrow{n},\overrightarrow{PC}$>=$\frac{\overrightarrow{n}•\overrightarrow{PC}}{|\overrightarrow{n}||\overrightarrow{PC}|}$=-$\frac{2\sqrt{2}}{3}$.
∴PC与平面PAB所成角的正弦值为$\frac{2\sqrt{2}}{3}$.
(III)∵M(0,2,0),∴$\overrightarrow{PB}$=(-1,4,-1),$\overrightarrow{CP}$=(1,0,1),$\overrightarrow{CM}$=(1,2,0).
设线段PB上存在点N使得平面CNM⊥平面PAB.
设$\overrightarrow{PN}=λ\overrightarrow{PB}$=(-λ,4λ,-λ),(0≤λ≤1).则$\overrightarrow{CN}$=$\overrightarrow{CP}+\overrightarrow{PN}$=(1-λ,4λ,1-λ).
设平面CNM的法向量为$\overrightarrow{m}$=(x,y,z),则$\left\{\begin{array}{l}{\overrightarrow{m}•\overrightarrow{CM}=0}\\{\overrightarrow{m}•\overrightarrow{CN}=0}\end{array}\right.$,
∴$\left\{\begin{array}{l}{x+2y=0}\\{(1-λ)x+4λy+(1-λ)z=0}\end{array}\right.$,设y=1得$\overrightarrow{m}$=(-2,1,$\frac{2-6λ}{1-λ}$).
∵平面CNM⊥平面PAB,∴$\overrightarrow{m}•\overrightarrow{n}=0$.
即-4+1+$\frac{4-12λ}{1-λ}$=0,解得$λ=\frac{1}{9}$.
∴线段PB上存在点N使得平面CNM⊥平面PAB,$\frac{PN}{PB}$=$\frac{1}{9}$.
点评 本题考查了线面垂直的判定与性质,线面角的计算,面面垂直的判定,属于中档题.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{4}$ | B. | 1 | C. | $\frac{4}{3}$ | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
| 年龄 | [5,15) | [15,25) | [25,35) | [35,45) | [45,55) | [55,65) |
| 频数 | 5 | 10 | 15 | 10 | 5 | 5 |
| 支持“生育二胎” | 4 | 5 | 12 | 8 | 2 | 1 |
| 年龄不低于45岁的人数 | 年龄低于45岁的人数 | 合计 | |
| 支持 | a= | c= | |
| 不支持 | b= | d= | |
| 合计 |
| P(K2≥k) | 0.050 | 0.010 | 0.001 |
| k | 3.841 | 6.635 | 10.828 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ±$\frac{\sqrt{3}}{3}$ | B. | ±$\sqrt{3}$ | C. | $\frac{\sqrt{3}}{3}$ | D. | $\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 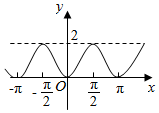 | B. | 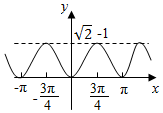 | ||
| C. | 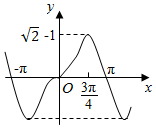 | D. | 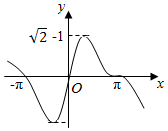 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
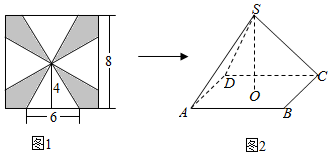 一块边长为8cm的正方形铁板按如图所示的阴影部分裁下,然后用余下的四个全等的等腰三角形加工成一个正四棱锥(底面是正方形,从顶点向底面作垂线,垂足为底面中心的四棱锥)形容器,O为底面ABCD的中心,则侧棱SC与底面ABCD所成角的余弦值为( )
一块边长为8cm的正方形铁板按如图所示的阴影部分裁下,然后用余下的四个全等的等腰三角形加工成一个正四棱锥(底面是正方形,从顶点向底面作垂线,垂足为底面中心的四棱锥)形容器,O为底面ABCD的中心,则侧棱SC与底面ABCD所成角的余弦值为( )| A. | $\frac{{2\sqrt{3}}}{5}$ | B. | $\frac{{3\sqrt{2}}}{5}$ | C. | $\frac{4}{5}$ | D. | $\frac{3}{5}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com