
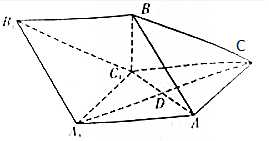
 如图,三棱柱ABC-A1B1C1中,AC=AA1=2,AB=BC=2$\sqrt{2}$,∠AA1C1=60°,平面ABC1⊥平面AA1C1C,AC1与A1C相交于点D.
如图,三棱柱ABC-A1B1C1中,AC=AA1=2,AB=BC=2$\sqrt{2}$,∠AA1C1=60°,平面ABC1⊥平面AA1C1C,AC1与A1C相交于点D.分析 (1)说明过B作平面AA1C1C的垂线,垂足在AC1上,取AC的中点E,连结CE,EB,说明过B作平面AA1C1C的垂线,垂足在EC1上,推出垂足是C1.然后证明结论.
(2)以点D为坐标原点,DA、DC、DM分别为x轴、y轴、z轴,建立空间直角坐标系,分别求出平面ABC1与平面ABC的法向量,从而可算出二面角C1-AB-C的余弦值.
解答 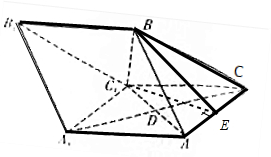 解:(1)∵三棱柱ABC-A1B1C1中,AC=AA1=2,AB=BC=2$\sqrt{2}$,∠AA1C1=60°,
解:(1)∵三棱柱ABC-A1B1C1中,AC=AA1=2,AB=BC=2$\sqrt{2}$,∠AA1C1=60°,
∵AC=AA1,∴AA1=A1C1,
∵∠AA1C1=60°,∴△AA1C1为等腰三角形,
同理△ABC1是等腰三角形,
∵D为AC1的中点,∴BD⊥AC1,
∵平面ABC1⊥平面AA1C1C,所以过B作平面AA1C1C的垂线,垂足在AC1上,
三角形ABC是等腰三角形,取AC的中点E,连结CE,EB,可知BE⊥AC,C1E⊥AC,所以AC⊥平面BEC1,
过B作平面AA1C1C的垂线,垂足在EC1上,可得垂足是C1.
∴BC1⊥平面AA1C1C.
(2)由(1)可得C1B=2,以点D为坐标原点,DA、DC、DM分别为x轴、y轴、z轴,建立空间直角坐标系,M为AB的中点,A(1,0,0);B(-1,0,2)C(0,$\sqrt{3}$,0),D(0,0,0),
平面ABC1的一个法向量为$\overrightarrow{m}$=(0,1,0),设平面ABC的法向量为$\overrightarrow{n}$=(x,y,z),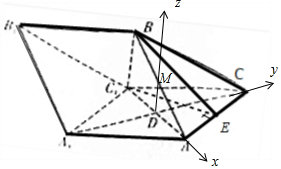
由题意可得$\overrightarrow{AC}$=(-1,$\sqrt{3}$,0),$\overrightarrow{AB}$=(-2,0,2),则$\left\{\begin{array}{l}{\overrightarrow{n}•\overrightarrow{AC}=-x+\sqrt{3}y=0}\\{\overrightarrow{n}•\overrightarrow{AB}=-2x+2z=0}\end{array}\right.$,
所以平面ABC的一个法向量为$\overrightarrow{n}$=($\sqrt{3}$,1,$\sqrt{3}$),
∴cosθ=$\frac{\overrightarrow{n}•\overrightarrow{m}}{|\overrightarrow{n}||\overrightarrow{m}|}$=$\frac{1}{1•\sqrt{7}}$=$\frac{\sqrt{7}}{7}$
即二面角C1-AB-C的余弦值等于$\frac{\sqrt{7}}{7}$.
点评 本题在三棱柱中求证线面垂直,并求二面角的平面角大小.着重考查了面面垂直的判定与性质、棱柱的性质、余弦定理、二面角的定义及求法等知识,属于中档题.


 名校通行证有效作业系列答案
名校通行证有效作业系列答案科目:高中数学 来源: 题型:选择题
 下面的茎叶图表示连续多天同一路口同一时段通过车辆的数目,则这些车辆数的中位数和众数分别是( )
下面的茎叶图表示连续多天同一路口同一时段通过车辆的数目,则这些车辆数的中位数和众数分别是( )| A. | 230.5,220 | B. | 231.5,232 | C. | 231,231 | D. | 232,231 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3-2\sqrt{2}}{8}$ | B. | $\frac{2-\sqrt{2}}{4}$ | C. | $\frac{5-2\sqrt{2}}{8}$ | D. | $\frac{5-2\sqrt{2}}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 某校高三文科班150名男生在“学生体质健康50米跑”单项测试中,成绩全部介于6秒与11秒之间.现将测试结果分成五组:第一组[6,7];第二组(7,8],…,第五组(10,11].如图是按上述分组方法得到的频率分布直方图.按国家标准,高三男生50米跑成绩小于或等于7秒认定为优秀,若已知第四组共48人,则该校文科班男生在这次测试中成绩优秀的人数是9.
某校高三文科班150名男生在“学生体质健康50米跑”单项测试中,成绩全部介于6秒与11秒之间.现将测试结果分成五组:第一组[6,7];第二组(7,8],…,第五组(10,11].如图是按上述分组方法得到的频率分布直方图.按国家标准,高三男生50米跑成绩小于或等于7秒认定为优秀,若已知第四组共48人,则该校文科班男生在这次测试中成绩优秀的人数是9.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
 工人在悬挂如图所示的一个正六边形装饰品时,需要固定六个位置上的螺丝,首先随意拧紧一个螺丝,接着拧紧距离它最远的第二个螺丝,再随意拧紧第三个螺丝,接着拧紧距离第三个螺丝最远的第四个螺丝,第五个和第六个以此类推,则不同的固定方式有48种.
工人在悬挂如图所示的一个正六边形装饰品时,需要固定六个位置上的螺丝,首先随意拧紧一个螺丝,接着拧紧距离它最远的第二个螺丝,再随意拧紧第三个螺丝,接着拧紧距离第三个螺丝最远的第四个螺丝,第五个和第六个以此类推,则不同的固定方式有48种.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 4 | D. | 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,四棱锥P-ABCD中,平面PAD⊥平面ABCD,底面ABCD为等腰梯形,AB∥CD,AD=DC=BC=2,AB=4,△PAD为正三角形.
如图,四棱锥P-ABCD中,平面PAD⊥平面ABCD,底面ABCD为等腰梯形,AB∥CD,AD=DC=BC=2,AB=4,△PAD为正三角形.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
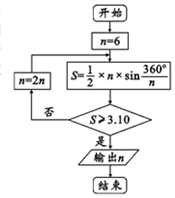 公元263年左右,我国数学家刘徽发现,当圆内接多边形的边数无限增加时,多边形面积可无限逼近圆的面积,由此创立了割圆术,利用割圆术刘徽得到了圆周率精确到小数点后面两位的近似值3.14,这就是著名的徽率.如图是利用刘徽的割圆术设计的程序框图,则输出的n值为( )
公元263年左右,我国数学家刘徽发现,当圆内接多边形的边数无限增加时,多边形面积可无限逼近圆的面积,由此创立了割圆术,利用割圆术刘徽得到了圆周率精确到小数点后面两位的近似值3.14,这就是著名的徽率.如图是利用刘徽的割圆术设计的程序框图,则输出的n值为( )| A. | 12 | B. | 24 | C. | 48 | D. | 96 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com