
| A. | $\frac{5}{7}$ | B. | $\frac{7}{10}$ | C. | $\frac{47}{70}$ | D. | $\frac{24}{35}$ |
分析 从10个不同的点中任取4个点的不同取法共有${C}_{10}^{4}$种,它可分为两类:4点共面与不共面.求出取出4个不共面的点的不同取法的种数,由此能求出这四个点不共面的概率.
解答 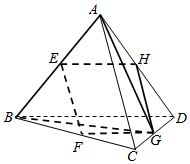 解:从10个不同的点中任取4个点的不同取法共有${C}_{10}^{4}$=210种,
解:从10个不同的点中任取4个点的不同取法共有${C}_{10}^{4}$=210种,
它可分为两类:4点共面与不共面.
如,4点共面的情形有三种:
①取出的4点在四面体的一个面内(如图中的AHGC在面ACD内),
这样的取法有$4{C}_{6}^{4}$种;
②取出的4面所在的平面与四面体的一组对棱平行(如图中的EFGH与AC、BD平行),
这种取法有3种(因为对棱共3组,即AC与BD、BC与AD、AB与CD);
③取出的4点是一条棱上的三点及对棱中点(如图中的AEBG),这样的取法共6种.
综上所述,取出4个不共面的点的不同取法的种数为${C}_{10}^{4}$-(4${C}_{6}^{4}$+3+6)=141种.
故这四个点不共面的概率为p=$\frac{141}{210}$=$\frac{47}{70}$.
故选:C.
点评 本题考查概率的求法,是中档题,解题时要认真审题,注意分类讨论思想、等可能事件概率计算公式的合理运用.


 天天向上口算本系列答案
天天向上口算本系列答案科目:高中数学 来源: 题型:解答题
 如图,斜三棱柱ABC-A1B1C1,面AA1B1B⊥面ABC,且∠A1AB=60°,AA1=2,△ABC为边长为2的等边三角形,G为△ABC的重心,取BC中点F,连接B1F与BC1交于E点:
如图,斜三棱柱ABC-A1B1C1,面AA1B1B⊥面ABC,且∠A1AB=60°,AA1=2,△ABC为边长为2的等边三角形,G为△ABC的重心,取BC中点F,连接B1F与BC1交于E点:查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1,0) | B. | (0,-1) | C. | (0,1) | D. | (-1,0) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 2$\sqrt{2}$ | B. | 2$\sqrt{3}$ | C. | 4$\sqrt{2}$ | D. | 4$\sqrt{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
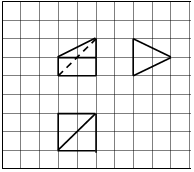 如图,网格纸上小正方形的边长为1,粗实线及粗虚线画出的是某多面体的三视图,则该多面体外接球的表面积为( )
如图,网格纸上小正方形的边长为1,粗实线及粗虚线画出的是某多面体的三视图,则该多面体外接球的表面积为( )| A. | 8π | B. | $\frac{25}{2}$π | C. | 12π | D. | $\frac{41}{4}$π |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | y=2e(x-1) | B. | y=ex-1 | C. | y=e(x-1) | D. | y=x-e |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com