
���� ��P��x��y���Ƴ�$\overrightarrow{P{F}_{1}}$$•\overrightarrow{P{F}_{2}}$=��-$\sqrt{5}$-x��-y����$\sqrt{5}$-x��-y��=x2+y2-5��ͨ����ֱ���������Сֵ���ɣ�
��� �⣺˫����$\frac{{x}^{2}}{4}$-$\frac{{y}^{2}}{{b}^{2}}$=1��b��0����������Ϊ$\frac{\sqrt{5}}{2}$��AΪ�㡢�ɵ�a=2����c=$\sqrt{5}$��b=$\sqrt{{c}^{2}-{a}^{2}}$=1��
��P��x��y����$\overrightarrow{P{F}_{1}}$$•\overrightarrow{P{F}_{2}}$=��-$\sqrt{5}$-x��-y����$\sqrt{5}$-x��-y��=x2+y2-5��
��Ȼ����OP��ABʱ��x2+y2ȡ����Сֵ����������ã�x2+y2��min=$\frac{4}{5}$���ʵ�P���߶�AB�ϣ�
��$\overrightarrow{P{F}_{1}}$•$\overrightarrow{P{F}_{2}}$����СֵΪ��$\frac{4}{5}-5=-\frac{21}{5}$��
�ʴ�Ϊ��-$\frac{21}{5}$��
���� ���⿼��˫���ߵļ����ʵ�Ӧ�ã��������������


 Сѧѧϰ�ð���ϵ�д�
Сѧѧϰ�ð���ϵ�д� Сѧͬ�����������ܾ�ϵ�д�
Сѧͬ�����������ܾ�ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
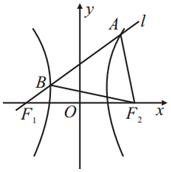 ��ͼ��F1��F2�ֱ�Ϊ˫����C��$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$��a��0��b��0�������ҽ��㣬��F1��ֱ��l��C��A��B���㣬��C��������Ϊ$\sqrt{7}$��|AB|=|AF2|����ֱ��l��б��Ϊ��������
��ͼ��F1��F2�ֱ�Ϊ˫����C��$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$��a��0��b��0�������ҽ��㣬��F1��ֱ��l��C��A��B���㣬��C��������Ϊ$\sqrt{7}$��|AB|=|AF2|����ֱ��l��б��Ϊ��������| A�� | $\frac{1}{2}$ | B�� | $\frac{{\sqrt{3}}}{3}$ | C�� | $\frac{{\sqrt{2}}}{2}$ | D�� | $\frac{{\sqrt{3}}}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1+$\frac{1}{2}$��2 | B�� | 1+$\frac{1}{2}$+$\frac{1}{3}$��3 | C�� | 1+$\frac{1}{2}$+$\frac{1}{3}$+$\frac{1}{4}$��3 | D�� | 1+$\frac{1}{2}$+$\frac{1}{3}$��2 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 �۲�ͼ�и�������ͼ����ÿ��������an��Բ�㣬��an��ͼ����Բ��ĸ�����an�����˹����ƶϳ�����Բ���ܺ�Sn��n�Ĺ�ϵʽΪ��������
�۲�ͼ�и�������ͼ����ÿ��������an��Բ�㣬��an��ͼ����Բ��ĸ�����an�����˹����ƶϳ�����Բ���ܺ�Sn��n�Ĺ�ϵʽΪ��������| A�� | ${S_n}=2{n^2}-2n$ | B�� | ${S_n}=2{n^2}$ | C�� | ${S_n}=4{n^2}-3n$ | D�� | ${S_n}=2{n^2}+2n$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
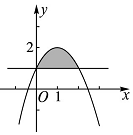
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com