Question

9．如图，函数y=-x²+2x+1与y=1相交形成一个封闭图形（图中的阴影部分），则该封闭图形的面积是$\frac{4}{3}$．

Answer 1

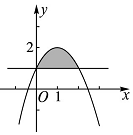
分析 本题考查的知识点是定积分的几何意义，首先我们要联立两个曲线的方程，判断他们的交点，以确定积分公式中x的取值范围，再根据定积分的几何意义，所求图形的面积为S=∫₀²（-x²+2x+1）dx-∫₀²1dx，计算后即得答案．

解答 解：函数y=-x²+2x+1与y=1的两个交点为（0，1）和（2，1），
所以封闭图形的面积等于S=∫₀²（-x²+2x+1）dx-∫₀²1dx
=∫₀²（-x²+2x+1-1）dx
=∫₀²（-x²+2x）dx
=（-$\frac{1}{3}{x}^{3}$+x²）|${\;}_{0}^{2}$=-$\frac{8}{3}$+4=$\frac{4}{3}$．
故答案为：$\frac{4}{3}$

点评 在直角坐标系下平面图形的面积的四个步骤：1．作图象；2．求交点；3．用定积分表示所求的面积；4．微积分基本定理求定积分．