
 ��ͼ����OA=6��AB=4�ľ���OABC������ƽ��ֱ������ϵ�У�����M��N��ÿ��1����λ���ٶȷֱ�ӵ�A��Cͬʱ���������е�M��AO���յ�O�˶�����N��CB���յ�B�˶��������������˶���t��ʱ������N��NP��BC����OB�ڵ�P������MP��
��ͼ����OA=6��AB=4�ľ���OABC������ƽ��ֱ������ϵ�У�����M��N��ÿ��1����λ���ٶȷֱ�ӵ�A��Cͬʱ���������е�M��AO���յ�O�˶�����N��CB���յ�B�˶��������������˶���t��ʱ������N��NP��BC����OB�ڵ�P������MP������ ��1�������⣬OA=6��AB=4������ֱ������ϵ�������ϵ�����������Ʊȿɵ�B��P�����꣮
��2��S��OMP=$\frac{1}{2}$��OM��PQ���ɵô𰸣�
��3���������⣬���ֱ��ON�ĺ�����ϵʽΪ��y=$\frac{4}{3}x$�����T������Ϊ��0��b�������ֱ��MT�ĺ�����ϵʽ�����������飬������꣮�ָ���������Σ����������������ʽ�����ONC���Ϊ$\frac{1}{3}$�����b��ֵ�Ƿ���ڼ��ɵý��ۣ�
��� �⣺��1�������⣬OA=6��AB=4��
��B��6��4����
�ӳ�NP��AB��Q��NB=6-t����OQ=t��
��QP=x����NP=4-x��
��OPQ�͡�NPB���ƣ���$\frac{6-t}{4-x}=\frac{t}{x}$
�ɵ�x=$\frac{2}{3}t$
��P��$t��\frac{2}{3}t$����
��2����S��OMP=$\frac{1}{2}$��OM��$\frac{2}{3}t$��
��S=$\frac{1}{2}$����6-t����$\frac{2}{3}t$=$-\frac{1}{3}$t2+2t=$-\frac{1}{3}��t-3��^{2}+3$��0��t��6����
�൱t=3ʱ��S�����ֵ��
��3�����ڣ�
�ɣ�2���ã���S�����ֵʱ����M��N������ֱ�Ϊ��M��3��0����N��3��4����
��ֱ��ON�ĺ�����ϵʽΪ��y=$\frac{4}{3}x$��
���T������Ϊ��0��b������ֱ��MT�ĺ�����ϵʽΪ��y=$-\frac{b}{3}x+b$��
�ⷽ����$\left\{\begin{array}{l}{y=\frac{4}{3}x}\\{y=-\frac{b}{3}x+b}\end{array}\right.$����$\left\{\begin{array}{l}x=\frac{3b}{4+b}\\ y=\frac{4b}{4+b}\end{array}\right.$
��ֱ��ON��MT�Ľ���R������Ϊ$��\frac{3b}{4+b}��\frac{4b}{4+b}��$��
��S��OCN=$\frac{1}{2}$��4��3=6����S��ORT=$\frac{1}{3}$S��OCN=2��
�ٵ���T�ڵ�O��C֮��ʱ����ʱT��ΪT1���ָ�����������ǡ�OR1T1��
��ͼ����R1D1��y�ᣬD1Ϊ���㣬��S��OR1T1=$\frac{1}{2}$R1D1•OT=$\frac{1}{2}$•$\frac{3b}{4+b}$•b=2��
��3b2-4b-16=0��b=$\frac{{2��2\sqrt{13}}}{3}$����b1=$\frac{{2+2\sqrt{13}}}{3}$��b2=$\frac{{2-2\sqrt{13}}}{3}$���������⣬��ȥ��
��ʱ��T1������Ϊ��0��$\frac{{2+2\sqrt{13}}}{3}$����
�ڵ���T��OC���ӳ�����ʱ���ָ�����������ǡ�R2NE����ͼ����MT��CN�ڵ�E��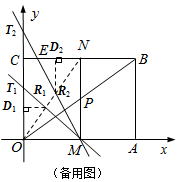
�ߵ�E��������Ϊ4�����ɢٵõ�E�ĺ�����Ϊ$\frac{3b-12}{b}$��
��R2D2��CN��CN�ڵ�D2����
S��R2NE=$\frac{1}{2}$•EN•D2=$\frac{1}{2}$•$��3-\frac{3b-12}{b}��$•$��4-\frac{4b}{4+b}��$=$\frac{96}{b��4+b��}$=2��
��b2+4b-48=0��b=$\frac{{-4��\sqrt{16+4��48}}}{2}=��2\sqrt{13}-2$��
��b1=$2\sqrt{13}$-2��b2=$-2\sqrt{13}-2$���������⣬��ȥ����
���ʱ��T2������Ϊ��0��$2\sqrt{13}-2$����
������������y���ϴ��ڵ�T1��0��$\frac{2+2\sqrt{13}}{3}$����T2��0��$\sqrt{13}-2$������������
���� ���⿼���˶��������������������亯������ʽ��������������Ĵ����ԣ��������⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
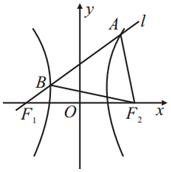 ��ͼ��F1��F2�ֱ�Ϊ˫����C��$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$��a��0��b��0�������ҽ��㣬��F1��ֱ��l��C��A��B���㣬��C��������Ϊ$\sqrt{7}$��|AB|=|AF2|����ֱ��l��б��Ϊ��������
��ͼ��F1��F2�ֱ�Ϊ˫����C��$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$��a��0��b��0�������ҽ��㣬��F1��ֱ��l��C��A��B���㣬��C��������Ϊ$\sqrt{7}$��|AB|=|AF2|����ֱ��l��б��Ϊ��������| A�� | $\frac{1}{2}$ | B�� | $\frac{{\sqrt{3}}}{3}$ | C�� | $\frac{{\sqrt{2}}}{2}$ | D�� | $\frac{{\sqrt{3}}}{2}$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
 �۲�ͼ�и�������ͼ����ÿ��������an��Բ�㣬��an��ͼ����Բ��ĸ�����an�����˹����ƶϳ�����Բ���ܺ�Sn��n�Ĺ�ϵʽΪ��������
�۲�ͼ�и�������ͼ����ÿ��������an��Բ�㣬��an��ͼ����Բ��ĸ�����an�����˹����ƶϳ�����Բ���ܺ�Sn��n�Ĺ�ϵʽΪ��������| A�� | ${S_n}=2{n^2}-2n$ | B�� | ${S_n}=2{n^2}$ | C�� | ${S_n}=4{n^2}-3n$ | D�� | ${S_n}=2{n^2}+2n$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | $\sqrt{2}$ | B�� | $\sqrt{3}$ | C�� | 2 | D�� | $\sqrt{6}$ |
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com