
分析 由已知函数$f(x)=lnx-2\sqrt{x}$,我们可以求出函数的导函数的解析式,判断出函数的单调性,进而得出当x=1时,函数f(x)取极大值,且为最大值.
解答 解:函数$f(x)=lnx-2\sqrt{x}$的导数为
f′(x)=$\frac{1}{x}$-$\frac{1}{\sqrt{x}}$=$\frac{1-\sqrt{x}}{x}$,
当x>1时,f′(x)<0,f(x)递减;当0<x<1时,f′(x)>0,f(x)递增.
可得f(x)在x=1处取得极大值,也为最大值,且f(1)=ln1-2=-2.
故答案为:-2.
点评 本题考查函数的最值的求法,注意运用导数,求出单调区间,可得极大值且为最大值,考查运算能力,属于基础题.


 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案科目:高中数学 来源: 题型:选择题
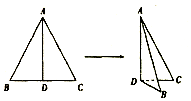 如图,将边长为2的正△ABC沿着高AD折起,使∠BDC=60°,若折起后A、B、C、D四点都在球O的表面上,则球O的表面积为( )
如图,将边长为2的正△ABC沿着高AD折起,使∠BDC=60°,若折起后A、B、C、D四点都在球O的表面上,则球O的表面积为( )| A. | $\frac{13}{2}π$ | B. | $\frac{13}{3}π$ | C. | $\frac{{13\sqrt{3}}}{2}π$ | D. | $\frac{{13\sqrt{3}}}{3}π$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ?a≥-1,ln(en+1)≤$\frac{1}{2}$ | B. | ?a<-1,ln(en+1)≤$\frac{1}{2}$ | C. | ?a≥-1,ln(en+1)≤$\frac{1}{2}$ | D. | ?a<-1,ln(en+1)≤$\frac{1}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com