
分析 (1)由题意可得c值,进一步求得椭圆上点A到右焦点的距离,由勾股定理求得A到左焦点的距离,再由椭圆定义求得a,由隐含条件求得b,则椭圆方程可求;
(2)假设椭圆上存在点P(x0,y0),使得PF1⊥PF2,由向量垂直与数量积的关系得到P点坐标的一个方程,与椭圆方程联立,由方程组无解说明椭圆上不存在一点P,使得PF1⊥PF2.
解答 解:(1)由题意可知,c=2,且|AF2|=3,则$|A{F}_{1}|=\sqrt{{3}^{2}+{4}^{2}}=5$,
∴2a=|AF1|+|AF2|=8,则a=4,
∴b2=a2-c2=12,
故椭圆方程为$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{12}=1$;
(2)假设椭圆上存在点P(x0,y0),使得PF1⊥PF2,
则$\overrightarrow{P{F}_{1}}•\overrightarrow{P{F}_{2}}=(-2-{x}_{0},-{y}_{0})•(2-{x}_{0},-{y}_{0})=0$,
即${{x}_{0}}^{2}+{{y}_{0}}^{2}=4$.
联立$\left\{\begin{array}{l}{{{x}_{0}}^{2}+{{y}_{0}}^{2}=4}\\{\frac{{{x}_{0}}^{2}}{16}+\frac{{{y}_{0}}^{2}}{12}=1}\end{array}\right.$,得:${{x}_{0}}^{2}=-32$,此方程无解.
∴椭圆上不存在一点P,使得PF1⊥PF2.
点评 本题考查了椭圆的定义求标准方程,考查椭圆的性质,考查向量垂直与数量积的关系,是中档题.


科目:高中数学 来源: 题型:解答题
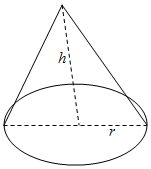 如图,某边路清扫机构为预备融化道路积雪,需要在冬天储备$\frac{500}{3}$π(m3)的工业食盐,其食盐堆成底面半径为r(m),高为h(m)的圆锥,并用防水材料S(m2)遮蔽食盐(不考虑接缝与重叠,即面积与圆锥侧面积相同)
如图,某边路清扫机构为预备融化道路积雪,需要在冬天储备$\frac{500}{3}$π(m3)的工业食盐,其食盐堆成底面半径为r(m),高为h(m)的圆锥,并用防水材料S(m2)遮蔽食盐(不考虑接缝与重叠,即面积与圆锥侧面积相同)查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 公差d>0 | B. | 当n=6时Sn最小 | ||
| C. | S13>0 | D. | 满足Sn<0的n有11个 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
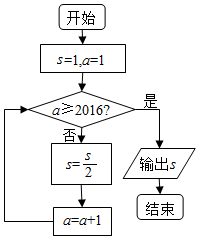
| A. | $\frac{1}{{2}^{2014}}$ | B. | $\frac{1}{{2}^{2015}}$ | C. | $\frac{1}{{2}^{2016}}$ | D. | $\frac{1}{{2}^{2017}}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com