
分析 (I)由于点M在线段AB上,满足|BM|=2|MA|,即$\overrightarrow{BM}=2\overrightarrow{MA}$,可得$\overrightarrow{OM}=\frac{1}{3}\overrightarrow{OB}+\frac{2}{3}\overrightarrow{OA}$.利用${k}_{OM}=\frac{\sqrt{5}}{10}$,可得$e=\frac{c}{a}=\sqrt{1-\frac{{b}^{2}}{{a}^{2}}}$.
(II)由(I)可得直线AB的方程为:$\frac{x}{\sqrt{5}b}+\frac{y}{b}$=1,利用中点坐标公式可得N.设点N关于直线AB的对称点为S$({x}_{1},\frac{7}{2})$,线段NS的中点T,又AB垂直平分线段NS,可得b,解得即可.
解答 解:(I)∵点M在线段AB上,满足|BM|=2|MA|,∴$\overrightarrow{BM}=2\overrightarrow{MA}$,
∵A(a,0),B(0,b),∴$\overrightarrow{OM}=\frac{1}{3}\overrightarrow{OB}+\frac{2}{3}\overrightarrow{OA}$=$(\frac{2}{3}a,\frac{1}{3}b)$.
∵${k}_{OM}=\frac{\sqrt{5}}{10}$,∴$\frac{b}{2a}=\frac{\sqrt{5}}{10}$,a=$\sqrt{5}$b.
∴$e=\frac{c}{a}=\sqrt{1-\frac{{b}^{2}}{{a}^{2}}}$=$\frac{2\sqrt{5}}{5}$.
(II)由(I)可得直线AB的方程为:$\frac{x}{\sqrt{5}b}+\frac{y}{b}$=1,N$(\frac{\sqrt{5}b}{2},-\frac{1}{2}b)$.
设点N关于直线AB的对称点为S$({x}_{1},\frac{7}{2})$,线段NS的中点T$(\frac{\sqrt{5}}{4}b+\frac{{x}_{1}}{2},-\frac{1}{4}b+\frac{7}{4})$,
又AB垂直平分线段NS,∴$\left\{\begin{array}{l}{\frac{\frac{\sqrt{5}b}{4}+\frac{1}{2}{x}_{1}}{\sqrt{5}b}+\frac{-\frac{1}{4}b+\frac{7}{4}}{b}=1}\\{\frac{\frac{7}{2}+\frac{1}{2}b}{{x}_{1}-\frac{\sqrt{5}}{2}b}=\sqrt{5}}\end{array}\right.$,解得b=3,
∴a=3$\sqrt{5}$.
∴椭圆E的方程为:$\frac{{x}^{2}}{45}+\frac{{y}^{2}}{9}=1$.
点评 本题考查了椭圆的标准方程及其性质、线段的垂直平分线性质、中点坐标公式、相互垂直的直线斜率之间的关系,考查了推理能力与计算能力,属于难题.


科目:高中数学 来源: 题型:填空题
 如图,已知圆C与x轴相切于点T(1,0),与y轴正半轴交于两点A,B(B在A的上方),且|AB|=2.
如图,已知圆C与x轴相切于点T(1,0),与y轴正半轴交于两点A,B(B在A的上方),且|AB|=2.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 命题①和命题②都成立 | B. | 命题①和命题②都不成立 | ||
| C. | 命题①成立,命题②不成立 | D. | 命题①不成立,命题②成立 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 恰有1个是奇数和全是奇数 | B. | 恰有1个是偶数和至少有1个是偶数 | ||
| C. | 至少有1个是奇数和全是奇数 | D. | 至少有1个是偶数和全是偶数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
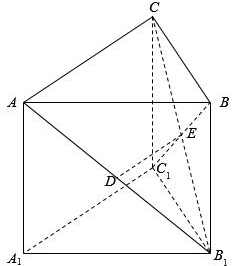 如图,在直三棱柱ABC-A1B1C1中,已知AC⊥BC,BC=CC1,设AB1的中点为D,B1C∩BC1=E.
如图,在直三棱柱ABC-A1B1C1中,已知AC⊥BC,BC=CC1,设AB1的中点为D,B1C∩BC1=E.查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 逐年比较,2008年减少二氧化硫排放量的效果最显著 | |
| B. | 2007年我国治理二氧化硫排放显现成效 | |
| C. | 2006年以来我国二氧化硫年排放量呈减少趋势 | |
| D. | 2006年以来我国二氧化硫年排放量与年份正相关 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | s≤$\frac{3}{4}$ | B. | s≤$\frac{5}{6}$ | C. | s≤$\frac{11}{12}$ | D. | s≤$\frac{25}{24}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com