
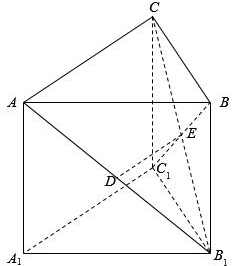
 如图,在直三棱柱ABC-A1B1C1中,已知AC⊥BC,BC=CC1,设AB1的中点为D,B1C∩BC1=E.
如图,在直三棱柱ABC-A1B1C1中,已知AC⊥BC,BC=CC1,设AB1的中点为D,B1C∩BC1=E.分析 (1)根据中位线定理得DE∥AC,即证DE∥平面AA1C1C;
(2)【方法一】先由直三棱柱得出CC1⊥平面ABC,即证AC⊥CC1;
再证明AC⊥平面BCC1B1,即证BC1⊥AC;
最后证明BC1⊥平面B1AC,即可证出BC1⊥AB1.
【方法二】建立空间直角坐标系,利用向量数量积证明异面直线垂直.
解答 证明:(1)根据题意,得;
E为B1C的中点,D为AB1的中点,所以DE∥AC;
又因为DE?平面AA1C1C,AC?平面AA1C1C,
所以DE∥平面AA1C1C;
(2)【方法一】因为棱柱ABC-A1B1C1是直三棱柱,
所以CC1⊥平面ABC,
因为AC?平面ABC,
所以AC⊥CC1;
又因为AC⊥BC,
CC1?平面BCC1B1,
BC?平面BCC1B1,
BC∩CC1=C,
所以AC⊥平面BCC1B1;
又因为BC1?平面BCC1B1,
所以BC1⊥AC;
因为BC=CC1,所以矩形BCC1B1是正方形,
所以BC1⊥平面B1AC;
又因为AB1?平面B1AC,
所以BC1⊥AB1.
【方法二】根据题意,A1C1⊥B1C1,CC1⊥平面A1B1C1,
以C1为原点建立空间直角座标系,
C1A1为x轴,C1B1为y轴,C1C为z轴,如图所示;
设BC=CC1=a,AC=b,
则A(b,0,a),B1(0,a,0),B(0,a,a),C1(0,0,0);
∴$\overrightarrow{{AB}_{1}}$=(-b,a,-a),$\overrightarrow{{BC}_{1}}$=(0,-a,-a),
∴$\overrightarrow{{AB}_{1}}$•$\overrightarrow{{BC}_{1}}$=-b×0+a×(-a)-a×(-a)=0,
∴$\overrightarrow{{AB}_{1}}$⊥$\overrightarrow{{BC}_{1}}$,
即AB1⊥BC1.
点评 本题考查了直线与直线,直线与平面以及平面与平面的位置关系,也考查了空间想象能力和推理论证能力的应用问题.


科目:高中数学 来源: 题型:选择题

| A. | 0 | B. | 2 | C. | 4 | D. | 14 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
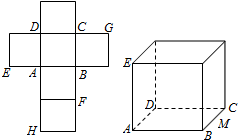 一个正方体的平面展开图及该正方体的直观图的示意图如图所示.在正方体中,设BC的中点为M、GH的中点为N.
一个正方体的平面展开图及该正方体的直观图的示意图如图所示.在正方体中,设BC的中点为M、GH的中点为N.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com