
分析 (I)f′(x)=$\frac{-3{x}^{2}+(6-a)x+a}{{e}^{x}}$,由f(x)在x=0处取得极值,可得f′(0)=0,解得a.可得f(1),f′(1),即可得出曲线y=f(x)在点(1,f(1))处的切线方程;
(II)解法一:由(I)可得:f′(x)=$\frac{-3{x}^{2}+(6-a)x+a}{{e}^{x}}$,令g(x)=-3x2+(6-a)x+a,由g(x)=0,解得x1=$\frac{6-a-\sqrt{{a}^{2}+36}}{6}$,x2=$\frac{6-a+\sqrt{{a}^{2}+36}}{6}$.对x分类讨论:当x<x1时;当x1<x<x2时;当x>x2时.由f(x)在[3,+∞)上为减函数,可知:x2=$\frac{6-a+\sqrt{{a}^{2}+36}}{6}$≤3,解得即可.
解法二:“分离参数法”:由f(x)在[3,+∞)上为减函数,可得f′(x)≤0,可得a≥$\frac{-3{x}^{2}+6x}{x-1}$,在[3,+∞)上恒成立.令u(x)=$\frac{-3{x}^{2}+6x}{x-1}$,利用导数研究其最大值即可.
解答 解:(I)f′(x)=$\frac{(6x+a){e}^{x}-(3{x}^{2}+ax){e}^{x}}{({e}^{x})^{2}}$=$\frac{-3{x}^{2}+(6-a)x+a}{{e}^{x}}$,
∵f(x)在x=0处取得极值,∴f′(0)=0,解得a=0.
当a=0时,f(x)=$\frac{3{x}^{2}}{{e}^{x}}$,f′(x)=$\frac{-3{x}^{2}+6x}{{e}^{x}}$,
∴f(1)=$\frac{3}{e}$,f′(1)=$\frac{3}{e}$,
∴曲线y=f(x)在点(1,f(1))处的切线方程为$y-\frac{3}{e}=\frac{3}{e}(x-1)$,化为:3x-ey=0;
(II)解法一:由(I)可得:f′(x)=$\frac{-3{x}^{2}+(6-a)x+a}{{e}^{x}}$,令g(x)=-3x2+(6-a)x+a,
由g(x)=0,解得x1=$\frac{6-a-\sqrt{{a}^{2}+36}}{6}$,x2=$\frac{6-a+\sqrt{{a}^{2}+36}}{6}$.
当x<x1时,g(x)<0,即f′(x)<0,此时函数f(x)为减函数;
当x1<x<x2时,g(x)>0,即f′(x)>0,此时函数f(x)为增函数;
当x>x2时,g(x)<0,即f′(x)<0,此时函数f(x)为减函数.
由f(x)在[3,+∞)上为减函数,可知:x2=$\frac{6-a+\sqrt{{a}^{2}+36}}{6}$≤3,解得a≥-$\frac{9}{2}$.
因此a的取值范围为:$[-\frac{9}{2},+∞)$.
解法二:由f(x)在[3,+∞)上为减函数,∴f′(x)≤0,
可得a≥$\frac{-3{x}^{2}+6x}{x-1}$,在[3,+∞)上恒成立.
令u(x)=$\frac{-3{x}^{2}+6x}{x-1}$,u′(x)=$\frac{-3[(x-1)^{2}+1]}{(x-1)^{2}}$<0,
∴u(x)在[3,+∞)上单调递减,
∴a≥u(3)=-$\frac{9}{2}$.
因此a的取值范围为:$[-\frac{9}{2},+∞)$.
点评 本题考查了导数的运算法则、利用导数的几何意义研究切线方程、利用导数研究函数的单调性极值,考查了分类讨论思想方法、“分离参数法”、推理能力与计算能力,属于难题.


 黄冈冠军课课练系列答案
黄冈冠军课课练系列答案科目:高中数学 来源: 题型:解答题
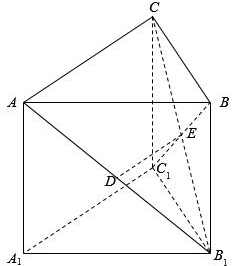 如图,在直三棱柱ABC-A1B1C1中,已知AC⊥BC,BC=CC1,设AB1的中点为D,B1C∩BC1=E.
如图,在直三棱柱ABC-A1B1C1中,已知AC⊥BC,BC=CC1,设AB1的中点为D,B1C∩BC1=E.查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | s≤$\frac{3}{4}$ | B. | s≤$\frac{5}{6}$ | C. | s≤$\frac{11}{12}$ | D. | s≤$\frac{25}{24}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [-3,1] | B. | (-3,1) | C. | (-∞,-3]∪[1,+∞) | D. | (-∞,-3)∪(1,+∞) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 11 | B. | 9 | C. | 5 | D. | 3 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com