
分析 (Ⅰ)由条件根据x=ρcosθ,y=ρsinθ求得C1,C2的极坐标方程.
(Ⅱ)把直线C3的极坐标方程代入ρ2-3$\sqrt{2}$ρ+4=0,求得ρ1和ρ2的值,结合圆的半径可得C2M⊥C2N,从而求得△C2MN的面积$\frac{1}{2}$•C2M•C2N的值.
解答 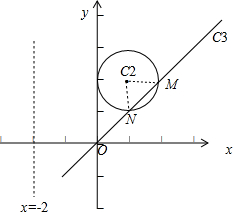 解:(Ⅰ)由于x=ρcosθ,y=ρsinθ,∴C1:x=-2 的
解:(Ⅰ)由于x=ρcosθ,y=ρsinθ,∴C1:x=-2 的
极坐标方程为 ρcosθ=-2,
故C2:(x-1)2+(y-2)2=1的极坐标方程为:
(ρcosθ-1)2+(ρsinθ-2)2=1,
化简可得ρ2-(2ρcosθ+4ρsinθ)+4=0.
(Ⅱ)把直线C3的极坐标方程θ=$\frac{π}{4}$(ρ∈R)代入
圆C2:(x-1)2+(y-2)2=1,
可得ρ2-(2ρcosθ+4ρsinθ)+4=0,
求得ρ1=2$\sqrt{2}$,ρ2=$\sqrt{2}$,
∴|MN|=|ρ1-ρ2|=$\sqrt{2}$,由于圆C2的半径为1,∴C2M⊥C2N,
△C2MN的面积为$\frac{1}{2}$•C2M•C2N=$\frac{1}{2}$•1•1=$\frac{1}{2}$.
点评 本题主要考查简单曲线的极坐标方程,点的极坐标的定义,属于基础题.


科目:高中数学 来源: 题型:选择题
| A. | 命题①和命题②都成立 | B. | 命题①和命题②都不成立 | ||
| C. | 命题①成立,命题②不成立 | D. | 命题①不成立,命题②成立 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
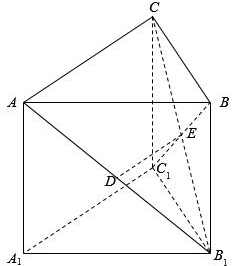 如图,在直三棱柱ABC-A1B1C1中,已知AC⊥BC,BC=CC1,设AB1的中点为D,B1C∩BC1=E.
如图,在直三棱柱ABC-A1B1C1中,已知AC⊥BC,BC=CC1,设AB1的中点为D,B1C∩BC1=E.查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 逐年比较,2008年减少二氧化硫排放量的效果最显著 | |
| B. | 2007年我国治理二氧化硫排放显现成效 | |
| C. | 2006年以来我国二氧化硫年排放量呈减少趋势 | |
| D. | 2006年以来我国二氧化硫年排放量与年份正相关 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{10}$ | B. | $\frac{1}{5}$ | C. | $\frac{1}{10}$ | D. | $\frac{1}{20}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [$-\frac{3}{2e},1$) | B. | [$-\frac{3}{2e},\frac{3}{4}$) | C. | [$\frac{3}{2e},\frac{3}{4}$) | D. | [$\frac{3}{2e},1$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | s≤$\frac{3}{4}$ | B. | s≤$\frac{5}{6}$ | C. | s≤$\frac{11}{12}$ | D. | s≤$\frac{25}{24}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com