
分析 (Ⅰ)a1=6,利用an+1=$\left\{\begin{array}{l}{2{a}_{n},}&{{a}_{n}≤18}\\{2{a}_{n}-36,}&{{a}_{n>18}}\end{array}\right.$可求得集合M的所有元素为6,12,24;
(Ⅱ)因为集合M存在一个元素是3的倍数,所以不妨设ak是3的倍数,由an+1=$\left\{\begin{array}{l}{2{a}_{n},}&{{a}_{n}≤18}\\{2{a}_{n}-36,}&{{a}_{n>18}}\end{array}\right.$(n=1,2,…),可归纳证明对任意n≥k,an是3的倍数;
(Ⅲ)分a1是3的倍数与a1不是3的倍数讨论,即可求得集合M的元素个数的最大值.
解答 解:(Ⅰ)若a1=6,由于an+1=$\left\{\begin{array}{l}{2{a}_{n},}&{{a}_{n}≤18}\\{2{a}_{n}-36,}&{{a}_{n>18}}\end{array}\right.$(n=1,2,…),M={an|n∈N*}.
故集合M的所有元素为6,12,24;
(Ⅱ)因为集合M存在一个元素是3的倍数,所以不妨设ak是3的倍数,由an+1=$\left\{\begin{array}{l}{2{a}_{n},}&{{a}_{n}≤18}\\{2{a}_{n}-36,}&{{a}_{n>18}}\end{array}\right.$(n=1,2,…),可归纳证明对任意n≥k,an是3的倍数.
如果k=1,M的所有元素都是3的倍数;
如果k>1,因为ak=2ak-1,或ak=2ak-1-36,所以2ak-1是3的倍数;于是ak-1是3的倍数;
类似可得,ak-2,…,a1都是3的倍数;
从而对任意n≥1,an是3的倍数;
综上,若集合M存在一个元素是3的倍数,则集合M的所有元素都是3的倍数
(Ⅲ)对a1≤36,an=$\left\{\begin{array}{l}2{a}_{n-1},&{a}_{n}≤18\\ 2{a}_{n-1}-36,&{a}_{n>18}\end{array}\right.$(n=1,2,…),可归纳证明对任意n≥k,an<36(n=2,3,…)
因为a1是正整数,a2=$\left\{\begin{array}{l}2{a}_{1},{a}_{1}≤18\\ 2{a}_{1}-36,{a}_{1}>18\end{array}\right.$,所以a2是2的倍数.
从而当n≥2时,an是2的倍数.
如果a1是3的倍数,由(Ⅱ)知,对所有正整数n,an是3的倍数.
因此当n≥3时,an∈{12,24,36},这时M的元素个数不超过5.
如果a1不是3的倍数,由(Ⅱ)知,对所有正整数n,an不是3的倍数.
因此当n≥3时,an∈{4,8,16,20,28,32},这时M的元素个数不超过8.
当a1=1时,M={1,2,4,8,16,20,28,32},有8个元素.
综上可知,集合M的元素个数的最大值为8.
点评 本题考查数列递推关系的应用,突出考查分类讨论思想与等价转化思想及推理、运算能力,属于难题.


科目:高中数学 来源: 题型:选择题
| A. | 恰有1个是奇数和全是奇数 | B. | 恰有1个是偶数和至少有1个是偶数 | ||
| C. | 至少有1个是奇数和全是奇数 | D. | 至少有1个是偶数和全是偶数 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
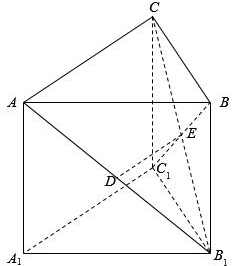 如图,在直三棱柱ABC-A1B1C1中,已知AC⊥BC,BC=CC1,设AB1的中点为D,B1C∩BC1=E.
如图,在直三棱柱ABC-A1B1C1中,已知AC⊥BC,BC=CC1,设AB1的中点为D,B1C∩BC1=E.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,在四棱锥P-ABCD中,已知PA⊥平面ABCD,且四边形ABCD为直角梯形,∠ABC=∠BAD=$\frac{π}{2}$,PA=AD=2,AB=BC=1.
如图,在四棱锥P-ABCD中,已知PA⊥平面ABCD,且四边形ABCD为直角梯形,∠ABC=∠BAD=$\frac{π}{2}$,PA=AD=2,AB=BC=1.查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | 逐年比较,2008年减少二氧化硫排放量的效果最显著 | |
| B. | 2007年我国治理二氧化硫排放显现成效 | |
| C. | 2006年以来我国二氧化硫年排放量呈减少趋势 | |
| D. | 2006年以来我国二氧化硫年排放量与年份正相关 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{3}{10}$ | B. | $\frac{1}{5}$ | C. | $\frac{1}{10}$ | D. | $\frac{1}{20}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com