
���� ��1����С�⿼���֪ʶ���ǹŵ���ͣ��ؼ���Ҫ�ҳ�������������$\overrightarrow{a}$•$\overrightarrow{b}$=-1�Ļ����¼����������ܵĻ����¼��ĸ������ٴ���ŵ����ʽ���м�����⣮
��2����С�⿼���֪ʶ���Ǽ��θ��͵����壬�ؼ���Ҫ��������������ͼ�Σ����ͼ�η������ҳ����������ĵ㼯��Ӧ��ͼ���������ͼ�ε��������
��� �⣺��1����һö�ʵؾ��ȵ������������Ⱥ��������Σ��������Ļ����¼�����Ϊ6��6=36����
��$\overrightarrow{a}$•$\overrightarrow{b}$=-1��-2x+y=-1����������a•b=-1�Ļ����¼�Ϊ��1��1������2��3������3��5������3����
������$\overrightarrow{a}$•$\overrightarrow{b}$=-1�ĸ���Ϊ$\frac{3}{36}$=$\frac{1}{12}$��
������x��y����������[1��6]��ȡֵ����ȫ�������¼��Ľ��Ϊ��={��x��y��|1��x��6��1��y��6}��
����$\overrightarrow{a}$•$\overrightarrow{b}$��0�Ļ����¼��Ľ��ΪA={��x��y��|1��x��6��1��y��6��-2x+y��0}��
����ͼ������ͼ��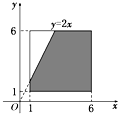
���ε����ΪS����=25����Ӱ���ֵ����ΪS��Ӱ=25-$\frac{1}{2}$��2��4=21��
������$\overrightarrow{a}$•$\overrightarrow{b}$��0�ĸ���Ϊ$\frac{21}{25}$��
���� ������Ҫ����ŵ���ʺͼ��θ��ͣ����������ν�ϵ���ѧ˼�룬�����е��⣮



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | [-$\frac{1}{6}$��$\frac{1}{6}$] | B�� | [-$\frac{\sqrt{6}}{6}$��$\frac{\sqrt{6}}{6}$] | C�� | [-$\frac{1}{3}$��$\frac{1}{3}$] | D�� | [-$\frac{\sqrt{3}}{3}$��$\frac{\sqrt{3}}{3}$] |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 1 | B�� | 2 | C�� | $\sqrt{3}$ | D�� | $\sqrt{3}+1$ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ͼ����ڵ�$��{-\frac{��}{6}��0}��$���ĶԳ� | B�� | ͼ�����$x=-\frac{��}{6}$��Գ� | ||
| C�� | ������$[{-\frac{5��}{12}��-\frac{��}{6}}]$�������� | D�� | ��$[{-\frac{��}{12}��\frac{5��}{12}}]$�������� |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | ��0��$\frac{1}{2}$�� | B�� | ��0��1�� | C�� | ��$\frac{1}{2}$��1�� | D�� | ∅ |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com