
已知函数f(x)= 在x=0,x=
在x=0,x=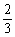 处存在极值。
处存在极值。
(1)求实数a, b的值;
(2)函数y=f(x)的图象上存在两点A, B使得△AOB是以坐标原点O为直角顶点的直角三角形,且斜边AB的中点在y轴上,求实数c的取值范围;
(3)当c=e时,讨论关于x的方程f(x)=kx (k∈R)的实根个数。
(1)当x<1时,f ' (x)=-3x2+2ax+b.
因为函数f(x)在x=0, x=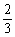 处存在极值,所以
处存在极值,所以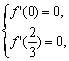
解得a=1, b=0. …………(3分)
(2)由(1)得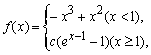
根据条件知A, B的横坐标互为相反数,不妨设A(-t, t3+t2), B(t, f(t)(t>0). … (4分)
若t<1,则f(t)=-t3+t2,
由∠AOB是直角得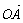 ·
·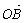 =0,即-t2+( t3+t2)(-t3+t2)=0,
=0,即-t2+( t3+t2)(-t3+t2)=0,
即t4-t2+1=0.此时无解; …………(5分)
若t≥1,则f(t)=c(et―1―1).由于AB的中点在y轴上,且∠AOB是直角,
所以B点不可能在x轴上,即t≠1.
同理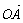 ·
·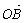 =0, 即-t2+( t3+t2)·c(et―1―1)=0,
=0, 即-t2+( t3+t2)·c(et―1―1)=0,
整理后得 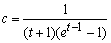 . …………(7分)
. …………(7分)
因为函数y=(t+1)(et-1―1)在t>1上的值域是(0, +∞),
所以实数c的取值范围是(0, +∞). …………(8分)
(3)由方程f(x)=kx,
知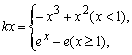
因为0一定是方程的根, …………(9分)
所以仅就x≠0时进行研究:
方程等价于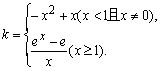
构造函数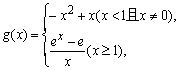 …………(10分)
…………(10分)
对于x<1且x≠0部分,函数g(x)=-x2+x的图象是开口向下的抛物线的一部分,当x= 时取得最大值
时取得最大值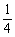 ,其值域是(-∞, 0)∪(0,
,其值域是(-∞, 0)∪(0, 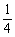 ]; …………(11分)
]; …………(11分)
对于x≥1部分,函数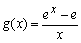 ,由
,由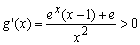 ,
,
知函数g(x)在(1, +∞)上单调递增,则g(x)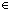 [0,+
[0,+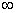 ) …………(13分)
) …………(13分)
所以, ①当k>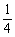 或k<0时,方程f(x)=kx有一个实根;
或k<0时,方程f(x)=kx有一个实根;
②当k=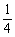 或k=0时,方程f(x)=kx有两个实根;
或k=0时,方程f(x)=kx有两个实根;
③当0<k<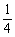 时,方程f(x)=kx有三个实根。 …………(14分)
时,方程f(x)=kx有三个实根。 …………(14分)


 课堂小作业系列答案
课堂小作业系列答案 黄冈小状元口算速算练习册系列答案
黄冈小状元口算速算练习册系列答案 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案科目:高中数学 来源: 题型:
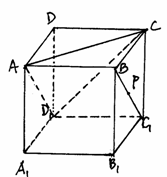
如图,正方体ABCD—A1B1C1D1,则下列四个命题:
①P在直线BC1上运动时,三棱锥A—D1PC的体积不变;
②P在直线BC1上运动时,直线AP与平面ACD1所成角的大小不变;
③P在直线BC1上运动时,二面角P—AD1—的大小不变;
④M是平面A1B1C1D1上到点D和C1距离相等的点,则M点的轨迹是过D1点的直线D1A1。
其中真命题的编号是 。
查看答案和解析>>
科目:高中数学 来源: 题型:
设D={(x, y)|(x-y)(x+y)≤0},记“平面区域D夹在直线y=-1与y=t(t∈[-1,1])之间的部分的面积”为S,则函数S=f(t)的图象的大致形状为
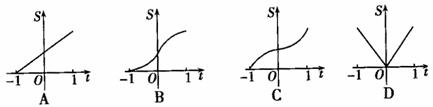
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)=2cos2x―sin(2x―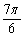 ).
).
(1)求函数f(x)的最大值,并写出f(x)取最大值时x的取值集合;
(2)已知△ABC中,角A, B, C的对边分别为a, b, c,若f(A)=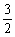 , b+c=2,求实数a的最小值。
, b+c=2,求实数a的最小值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com