
已知函数f(x)=2cos2x―sin(2x―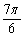 ).
).
(1)求函数f(x)的最大值,并写出f(x)取最大值时x的取值集合;
(2)已知△ABC中,角A, B, C的对边分别为a, b, c,若f(A)=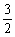 , b+c=2,求实数a的最小值。
, b+c=2,求实数a的最小值。
(1)f(x)=2cos2x-sin(2x-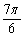 )=(1+cos2x)-(sin2xcos
)=(1+cos2x)-(sin2xcos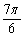 -cos2xsin
-cos2xsin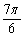 )
)
=1+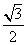 sin2x+
sin2x+ cos2x=sin(2x+
cos2x=sin(2x+ )+1 …………(3分)
)+1 …………(3分)
所以函数f(x)的最大值为2. …………(4分)
此时sin(2x+ )=1,即2x+
)=1,即2x+ =2kπ+
=2kπ+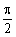 (k
(k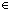 z) 解得x=kπ+
z) 解得x=kπ+ (k
(k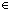 z)
z)
故x的取值集合为 {x| x=kπ+
{x| x=kπ+ ,k
,k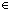 z} …………(6分)
z} …………(6分)
(2)由题意f(A)=sin(2A+ )+1=
)+1=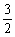 ,化简得sin(2A+
,化简得sin(2A+ )=
)= ,
,
∵A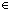 (0,π),
(0,π),  2A+
2A+
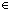 (
( ,
,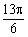 ).
).  A=
A=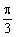 …………(8分)
…………(8分)
在三角形ABC中,根据余弦定理,
得a2=b2+c2-2bc·cos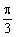 =(b+c)2-3bc …………(10分)
=(b+c)2-3bc …………(10分)
由b+c=2 知bc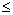 (
( )2=1, 即a2
)2=1, 即a2 1
1
 当b=c=1时,实数a的最小值为1. …………(12分)
当b=c=1时,实数a的最小值为1. …………(12分)


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
P是双曲线 右支上的一点,M, N分别是圆(x+5)2+y2=4和
右支上的一点,M, N分别是圆(x+5)2+y2=4和
(x-5)2+y2=1上的点,则|PM|-|PN|的最大值为
A.6 B.7 C.8 D.9
查看答案和解析>>
科目:高中数学 来源: 题型:
已知f(n)=1+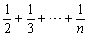 (n∈N*),经计算得f(4)>2, f(8)>
(n∈N*),经计算得f(4)>2, f(8)>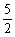 , f(16)>3, f(32)>
, f(16)>3, f(32)> ,
,
……,观察上述结果,则可归纳出一般结论为 。
查看答案和解析>>
科目:高中数学 来源: 题型:
已知函数f(x)= 在x=0,x=
在x=0,x=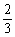 处存在极值。
处存在极值。
(1)求实数a, b的值;
(2)函数y=f(x)的图象上存在两点A, B使得△AOB是以坐标原点O为直角顶点的直角三角形,且斜边AB的中点在y轴上,求实数c的取值范围;
(3)当c=e时,讨论关于x的方程f(x)=kx (k∈R)的实根个数。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com