
分析 (I)把要解的不等式等价转化为与之等价的三个不等式组,求出每个不等式组的解集,再取并集,即得所求.
(Ⅱ)由题意可得|a+1|>0,|b|-1>0,化简f(ab)-[f(a)-f(-b)]为|a+1|•(|b|-1|)>0,从而证得不等式成立.
解答 解:(I)不等式f(x)<|2x+1|-1,即|x+1|<|2x+1|-1,
∴$\left\{\begin{array}{l}{x<-1}\\{-x-1<-2x-1-1}\end{array}\right.$①,或 $\left\{\begin{array}{l}{-1≤x≤-\frac{1}{2}}\\{x+1<-2x-1-1}\end{array}\right.$②,或$\left\{\begin{array}{l}{x>-\frac{1}{2}}\\{x+1<2x+1-1}\end{array}\right.$③.
解①求得x<-1;解②求得x∈∅;解③求得x>1.
故要求的不等式的解集M={x|x<-1或 x>1}.
(Ⅱ)证明:设a,b∈M,∴|a+1|>0,|b|-1>0,
则 f(ab)=|ab+1|,f(a)-f(-b)=|a+1|-|-b+1|.
∴f(ab)-[f(a)-f(-b)]=f(ab)+f(-b)-f(a)=|ab+1|+|1-b|-|a+1|
=|ab+1|+|b-1|-|a+1|≥|ab+1+b-1|-|a+1|=|b(a+1)|-|a+1|
=|b|•|a+1|-|a+1|=|a+1|•(|b|-1|)>0,
故f(ab)>f(a)-f(-b)成立.
点评 本题主要考查绝对值不等式的解法,绝对值三角不等式,属于中档题.


 黄冈小状元解决问题天天练系列答案
黄冈小状元解决问题天天练系列答案 三点一测快乐周计划系列答案
三点一测快乐周计划系列答案科目:高中数学 来源: 题型:选择题
 如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a,b分别为4,10,则输出的a为( )
如图程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执行该程序框图,若输入的a,b分别为4,10,则输出的a为( )| A. | 0 | B. | 2 | C. | 4 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{7}{3}$ | B. | 2 | C. | $\frac{3}{2}$ | D. | $\frac{4}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
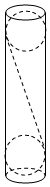 如图所示,一个圆乒乓球筒,高为20厘米,底面半径为2厘米,球桶的上底和下底分别粘有一个乒乓球,乒乓球与球筒底面及侧面均相切(球筒和乒乓球厚度均忽略不计),一个平面与两个乒乓球均相切,且此平面截球筒边缘所得的图形为一个椭圆,则该椭圆的离心率为( )
如图所示,一个圆乒乓球筒,高为20厘米,底面半径为2厘米,球桶的上底和下底分别粘有一个乒乓球,乒乓球与球筒底面及侧面均相切(球筒和乒乓球厚度均忽略不计),一个平面与两个乒乓球均相切,且此平面截球筒边缘所得的图形为一个椭圆,则该椭圆的离心率为( )| A. | $\frac{1}{5}$ | B. | $\frac{\sqrt{15}}{4}$ | C. | $\frac{2\sqrt{6}}{5}$ | D. | $\frac{1}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
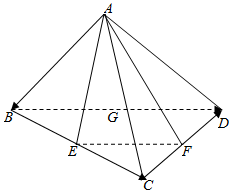 如图所示,已知空间四边形ABCD,连接AC,BD,E,F,G分别是BC,CD,DB的中点,请化简:
如图所示,已知空间四边形ABCD,连接AC,BD,E,F,G分别是BC,CD,DB的中点,请化简:查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题

| A. | $\frac{199}{200}$ | B. | $\frac{197}{198}$ | C. | $\frac{197}{199}$ | D. | $\frac{198}{199}$ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com