
若数列{an}满足a1=2且an+an-1=2n+2n-1,Sn为数列{an}的前n项和,则log2(S2012+2)等于( )
(A)2013 (B)2012 (C)2011 (D)2010
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:高中数学 来源: 题型:
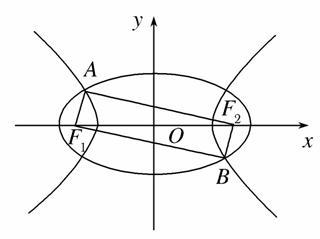
如图,F1,F2是椭圆C1: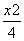 +y2=1与双曲线C2的公共焦点,A,B分别是C1,C2在第二、四象限的公共点.若四边形AF1BF2为矩形,则C2的离心率是( )
+y2=1与双曲线C2的公共焦点,A,B分别是C1,C2在第二、四象限的公共点.若四边形AF1BF2为矩形,则C2的离心率是( )
A.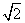 B.
B.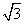 C.
C.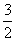 D.
D.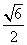
查看答案和解析>>
科目:高中数学 来源: 题型:
数列{an}的前n项和记为Sn,a1=t,点(Sn,an+1)在直线y=3x+1上,n∈N*.
(1)当实数t为何值时,数列{an}是等比数列?
(2)在(1)的结论下,设bn=log4an+1,cn=an+bn,Tn是数列{cn}的前n项和,求Tn.
查看答案和解析>>
科目:高中数学 来源: 题型:
给定函数①y=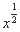 ,②y=
,②y=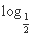 (x+1),③y=|x-1|,④y=2x+1,其中在区间(0,1)上单调递减的函数的序号是( )
(x+1),③y=|x-1|,④y=2x+1,其中在区间(0,1)上单调递减的函数的序号是( )
(A)①② (B)②③
(C)③④ (D)①④
查看答案和解析>>
科目:高中数学 来源: 题型:
下列函数中,既是偶函数,又在区间(1,2)内是增函数的为( )
(A)y=cos 2x,x∈R
(B)y=log2|x|,x∈R且x≠0
(C)y= ,x∈R
,x∈R
(D)y=x3+1,x∈R
查看答案和解析>>
科目:高中数学 来源: 题型:
幂函数y=x-1及直线y=x,y=1,x=1将平面直角坐标系的第一象限分成八个“卦限”:①,②,③,④,⑤,⑥,⑦,⑧(如图所示),那么幂函数y=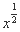 的图象经过的“卦限”是( )
的图象经过的“卦限”是( )
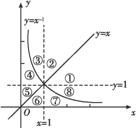
(A)④⑦ (B)④⑧ (C)③⑧ (D)①⑤
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com