
分析 (1)求出f′(x),令f′(x)=0,根据a的范围讨论f(x)的极值点和单调区间.
(2)对a的范围进行讨论,只需令f(x)在(-∞,0)上的最大值大于(0,+∞)上的最小值即可.
解答 解:(1)f(x)的定义域为{x|x≠0}.
f′(x)=aeax($\frac{a}{x}$+a+1)-eax•$\frac{a}{{x}^{2}}$=eax•$\frac{a[(a+1){x}^{2}+ax-1]}{{x}^{2}}$
①若a=0,则f(x)=1,∴f(x)无单调区间.
②若a≠0,令f′(x)=0得(a+1)x2+ax-1=0,
(i)若a=-1,则-x-1=0,x=-1,
当x<-1时,f′(x)<0,当-1<x<0或x>0时,f′(x)>0,
∴f(x)的增区间是(-1,0),(0,+∞),f(x)的减区间是(-∞,-1).
若a≠-1,令f′(x)=0,解得x=-1或x=$\frac{1}{a+1}$.
(ii)若-1<a<0,当x<-1或x>$\frac{1}{a+1}$时,f′(x)<0,当-1<x<0,或0$<x<\frac{1}{a+1}$时,f′(x)>0.
∴f(x)的增区间是(-1,0),(0,$\frac{1}{a+1}$),f(x)的减区间是(-∞,-1),($\frac{1}{a+1}$,+∞).
(iii)若a>0,当x<-1或x>$\frac{1}{a+1}$时,f′(x)>0,当-1<x<0,或0$<x<\frac{1}{a+1}$时,f′(x)<0.
∴f(x)的减区间是(-1,0),(0,$\frac{1}{a+1}$),f(x)的增区间是(-∞,-1),($\frac{1}{a+1}$,+∞).
(2)①当a=0时,f(x)=1,显然不符合题意;
②当a=-1时,f(x)=-$\frac{1}{x{e}^{x}}$,∴当x>0时,f(x)<0,当x<0时,f(x)>0,显然符合题意;
③当-1<a<0时,f(x)在(-∞,-1)上单调递减,在(-1,0)上单调递增,在(0,$\frac{1}{a+1}$)上单调递增,在($\frac{1}{a+1}$,+∞)上单调递减,
f(-1)=e-a>0,而x→0+时,f(x)→-∞,故必存在x1>0,x2<0,使f(x1)<f(x2);
④当a>0时,f(x)在(-∞,-1)上单调递增,在(-1,0)上单调递减,在(0,$\frac{1}{a+1}$)上单调递减,在($\frac{1}{a+1}$,+∞)上单调递增.
∴当x<0时,f(x)≤f(-1)=e-a,当x>0时,f(x)≥f($\frac{1}{a+1}$)=e${\;}^{\frac{a}{a+1}}$(a+1)2.
∵存在x1>0,x2<0,使f(x1)<f(x2).∴e-a>e${\;}^{\frac{a}{a+1}}$(a+1)2.
∵a>0,∴e-a<1,$\frac{a}{a+1}$>0,(a+1)2>1,∴e${\;}^{\frac{a}{a+1}}$(a+1)2>e${\;}^{\frac{a}{a+1}}$>1,∴e-a>e${\;}^{\frac{a}{a+1}}$(a+1)2无解.
综上,a的取值范围是[-1,0).
点评 本题考查了导数与函数的单调性的关系,函数极值的应用,分类较多,属于难题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
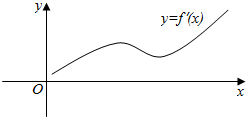 定义在全体正实数上的函数f(4)=1,f′(x)为f(x)的导函数,已知函数y=f′(x)的图象如图所示lnb≥ln2a且f(2a+b)≥1,则$\frac{3b+6}{2a+4}$的取值范围是( )
定义在全体正实数上的函数f(4)=1,f′(x)为f(x)的导函数,已知函数y=f′(x)的图象如图所示lnb≥ln2a且f(2a+b)≥1,则$\frac{3b+6}{2a+4}$的取值范围是( )| A. | [1,+∞] | B. | [2,+∞] | C. | [$\frac{3}{4}$,2] | D. | [0,3] |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -2 | B. | -3 | C. | -4 | D. | -5 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x)=$\frac{x-1}{{x}^{2}-1}$,g(x)=$\frac{1}{1+x}$ | B. | f(x)=($\sqrt{x}$)2,g(x)=$\sqrt{{x}^{2}}$ | ||
| C. | f(x)=$\root{3}{{x}^{4}-{x}^{3}}$,g(x)=x$\root{3}{x-1}$ | D. | f(x)=1,g(x)=sin(arcsinx) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com