
【题目】已知椭圆E的右焦点与抛物线y2=4x的焦点重合,点M ![]() 在椭圆E上. (Ⅰ)求椭圆E的标准方程;
在椭圆E上. (Ⅰ)求椭圆E的标准方程;
(Ⅱ)设P(﹣4,0),直线y=kx+1与椭圆E交于A,B两点,若直线PA,PB关于x轴对称,求k的值.
【答案】解:(Ⅰ)因为抛物线焦点为(1,0),所以椭圆的焦点坐标为F2(1,0),F1(﹣1,0),
又因为M(1, ![]() )在椭圆上,
)在椭圆上,
所以2a=|MF1|+|MF2|= ![]() +
+ ![]() =4,
=4,
即a=2,又因为c=1 所以b2=a2﹣c2=3,
所以椭圆的方程是 ![]() +
+ ![]() =1;
=1;
(Ⅱ)若直线PA,PB关于x轴对称,则kPA+kPB=0,
设A(x1,kx1+1),B(x2,kx2+1),
∴ ![]() ,
,
联立 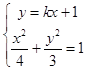 ,消去y得到(3+4k2)x2+8kx﹣8=0,
,消去y得到(3+4k2)x2+8kx﹣8=0,
∴ ![]() ,
,
∴ ![]() ,
,
即﹣16k﹣32k2﹣8k+24+32k2=0,
∴k=1
【解析】(Ⅰ)求出抛物线的焦点,可得椭圆的焦点,由椭圆的定义,运用两点的距离公式可得2a=4,即a=2,再由a,b,c的关系,可得b,进而得到椭圆方程;(Ⅱ)若直线PA,PB关于x轴对称,则kPA+kPB=0,设A(x1,kx1+1),B(x2,kx2+1),运用直线的斜率公式,联立直线方程和椭圆方程,运用韦达定理,化简整理可得k的方程,解方程即可得到k的值.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:高中数学 来源: 题型:
【题目】锐角△ABC中,角A、B、C所对的边分别为a、b、c,且tanA﹣tanB= ![]() (1+tanAtanB). (Ⅰ)若c2=a2+b2﹣ab,求角A、B、C的大小;
(1+tanAtanB). (Ⅰ)若c2=a2+b2﹣ab,求角A、B、C的大小;
(Ⅱ)已知向量 ![]() =(sinA,cosA),
=(sinA,cosA), ![]() =(cosB,sinB),求|3
=(cosB,sinB),求|3 ![]() ﹣2
﹣2 ![]() |的取值范围.
|的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】综合题。
(1)已知f( ![]() +1)=x+2
+1)=x+2 ![]() ,求f(x)的解析式;
,求f(x)的解析式;
(2)已知f(x)是一次函数,且满足3f(x+1)﹣2f(x﹣1)=2x+17,求f(x)的解析式.
查看答案和解析>>
科目:高中数学 来源: 题型:
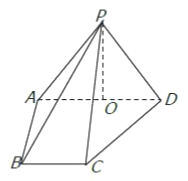
【题目】如图,在四棱锥![]() 中,侧面
中,侧面![]() 底面
底面![]() ,侧棱
,侧棱![]() ,底面
,底面![]() 为直角梯形,其中
为直角梯形,其中![]() 为
为![]() 中点.
中点.
(1)求证: ![]() 平面
平面![]() ;
;
(2)求异面直线![]() 与
与![]() 所成角的余弦值;
所成角的余弦值;
(3)线段![]() 上是否存在
上是否存在![]() ,使得它到平面
,使得它到平面![]() 的距离为
的距离为![]() ?若存在,求出
?若存在,求出![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某城市在发展过程中,交通状况逐渐受到有关部门的关注,据有关统计数据显示,从上午6点到中午12点,车辆通过该市某一路段的用时y(分钟)与车辆进入该路段的时刻t之间的关系可近似地用如下函数给出: y= 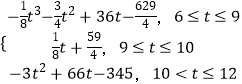
求从上午6点到中午12点,通过该路段用时最多的时刻.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义:若函数![]() 的定义域为
的定义域为![]() ,且存在非零常数
,且存在非零常数![]() ,对任意
,对任意![]() ,
, ![]() 恒成立,则称
恒成立,则称![]() 为线周期函数,
为线周期函数, ![]() 为
为![]() 的线周期.
的线周期.
(Ⅰ)下列函数①![]() ,②
,②![]() ,③
,③![]() (其中
(其中![]() 表示不超过
表示不超过![]() 的最大整数),是线周期函数的是(直接填写序号);
的最大整数),是线周期函数的是(直接填写序号);
(Ⅱ)若![]() 为线周期函数,其线周期为
为线周期函数,其线周期为![]() ,求证:函数
,求证:函数![]() 为周期函数;
为周期函数;
(Ⅲ)若![]() 为线周期函数,求
为线周期函数,求![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com