
分析 (1)由条件利用任意角的三角函数的定义求得sinβ、cosβ的值,再利用二倍角公式求得sin2β的值.
(2)由条件利用余弦函数的周期性和最值求得函数f(x)的最大值和周期,再利用两角差的余弦公式求得f(β)的值.
解答 解:(1)平面直角坐标系xOy中,已知角β的顶点为坐标原点O,始边在x轴的正半轴上,终边经过点P(-4,3)
∴x=-4,y=3,r=|OP|=5,∴sinβ=$\frac{y}{r}$=$\frac{3}{5}$,cosβ=$\frac{x}{r}$=-$\frac{4}{5}$,
∴sin2β=2sinβcosβ=-$\frac{24}{25}$.
(2)∵已知函数f(x)=3cos(x-$\frac{π}{4}$),故函数f(x)的最大值为3,
最小正周期为2π,f(β)=3cos(β-$\frac{π}{4}$)=3cosβcos$\frac{π}{4}$+3sinβsin$\frac{π}{4}$=-$\frac{3\sqrt{2}}{10}$.
点评 本题主要考查任意角的三角函数的定义,二倍角公式;余弦函数的周期性和最值,两角差的余弦公式,属于基础题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
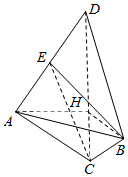 如图,在Rt△ACD中,AH⊥CD,H为垂足,CD=4,AD=2$\sqrt{3}$,∠CAD=90°,以CD为轴,将△ACD按逆时针方向旋转90°到△BCD位置,E为AD中点;
如图,在Rt△ACD中,AH⊥CD,H为垂足,CD=4,AD=2$\sqrt{3}$,∠CAD=90°,以CD为轴,将△ACD按逆时针方向旋转90°到△BCD位置,E为AD中点;查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com