考点:直线与平面所成的角,异面直线及其所成的角
专题:计算题,空间位置关系与距离,空间角
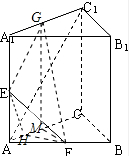
分析:(1)由AC1与底面成60°角,求出侧棱长,取A1C1的中点G,连接EG,FG,则EG∥AC1,则∠FEG或补角即为异面直线EF与AC1所成角.分别求出三角形FEG的三边,再由余弦定理,即可得到;
(2)在三角形ABC内,过F作FH⊥AC,由于平面ABC⊥平面ACC1A1,则FH⊥平面ACC1A1,即有∠FEH即为EF与平面ACC1A1所成角.通过解直角三角形EFH,即可得到.
解答:
解:(1)由于CC
1⊥平面ABC,则∠C
1AC=60°,
AC=2,则C
1C=ACtan60°=2
,
取A
1C
1的中点G,连接EG,FG,则EG∥AC
1,
则∠FEG或补角即为异面直线EF与AC
1所成角.
易得EF=
=2,EG=2,
再取AC的中点M,连接MG,MF,则FG=
=
,
则cos∠FEG=
=-
,
则有异面直线EF与AC
1所成角为arccos
;
(2)在三角形ABC内,过F作FH⊥AC,
由于平面ABC⊥平面ACC
1A
1,
则FH⊥平面ACC
1A
1,
即有∠FEH即为EF与平面ACC
1A
1所成角.
在直角三角形AFH中,FH=AFsin60°=
,
又EF=2,则sin∠FEH=
=
,
则EF与平面ACC
1A
1所成角的大小为arcsin
.
点评:本题主要考查空间异面直线所成的角和直线与平面所成的角,考查空间的直线与平面的位置关系,考查运算和推理能力,属于中档题.

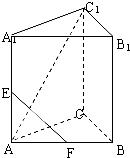 如图,在正三棱柱ABC-A1B1C1中,AC=2,AC1与底面成60°角,E、F分别为AA1、AB的中点.
如图,在正三棱柱ABC-A1B1C1中,AC=2,AC1与底面成60°角,E、F分别为AA1、AB的中点. 解:(1)由于CC1⊥平面ABC,则∠C1AC=60°,
解:(1)由于CC1⊥平面ABC,则∠C1AC=60°,
